Principles of Mathematical Induction Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. NCERT Solutions for Class 11 Maths Chapter 4 Principles of Mathematical Induction All Exercises were prepared by Experienced LearnCBSE.in Teachers.

Free download NCERT Solutions for Class 11 Maths Chapter 4 Principles of Mathematical Induction Ex 4.1 and Miscellaneous Exercise PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

NCERT Solutions for Class 11 Maths Chapter 4 Principle of Mathematical Induction

Topics and Sub Topics in Class 11 Maths Chapter 4 Principle of Mathematical Induction:

Section Name	Topic Name
4	Principle of Mathematical Induction
4.1	Introduction
4.2	Motivation
4.3	The Principle of Mathematical Induction

NCERT Solutions for Class 11 Maths Chapter 4 Exercise 4.1

Ex 4.1 Class 11 Maths Question 1:

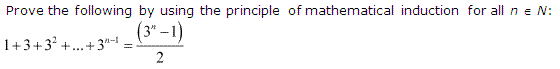
Ans :

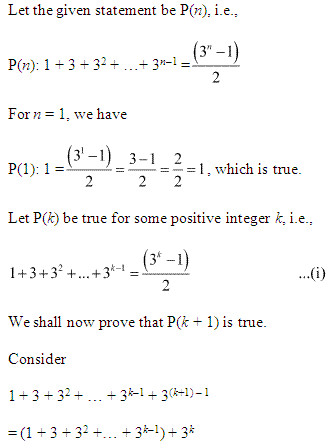
Ex 4.1 Class 11 Maths Question 2:

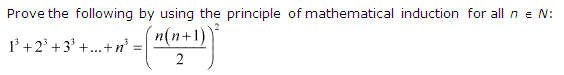
Ans :

Let the given statement be P(n), i.e.,

P(n) = 1³ + 2³ + 3³ + …………. + n³ = (n(n+1)2)2.
For n = 1, we have
P(1) : 1³ = 1
= (1(1+1)2)2=(122)2
= 1² = 1 which is true.
Let P(k) be true for some positive integer k, i.e.,
1³ + 2³ + 3³ + …………. + k³ = (k(k+1)2)2
We shall now prove that P(k+1) is true.
Consider 1³ + 2³ + 3³ + …………. + k³ = (k(k+1)2)2

NCERT Solutions For Class 11 Maths(Download PDF)

Ex 4.1 Class 11 Maths Question 3:

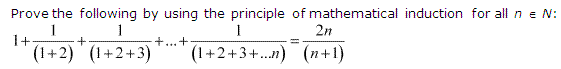
Ans :

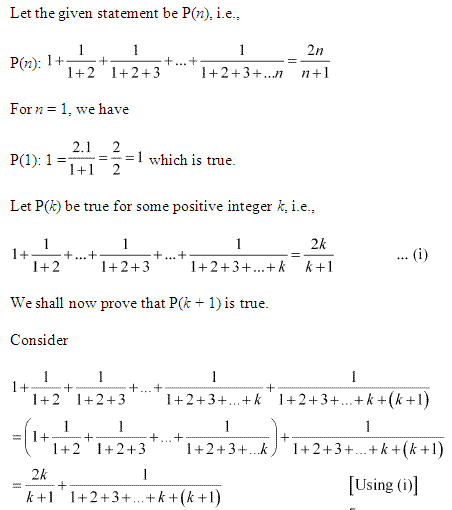
Ex 4.1 Class 11 Maths Question 4:

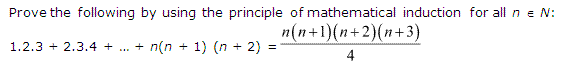
Ans :

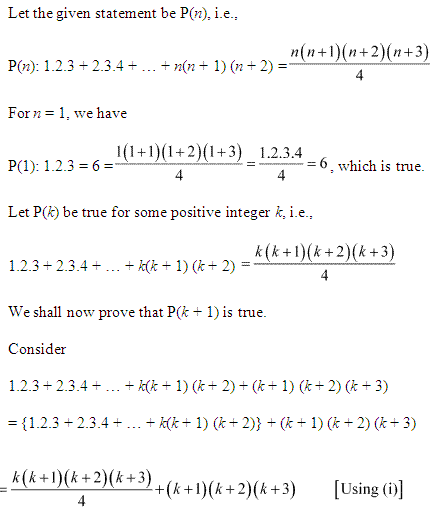
Ex 4.1 Class 11 Maths Question 5:

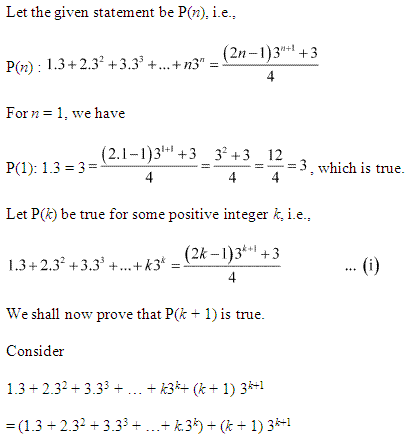
Ans :

Ex 4.1 Class 11 Maths Question 6:

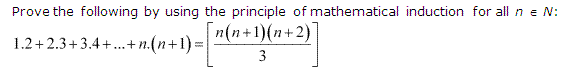
Ans :

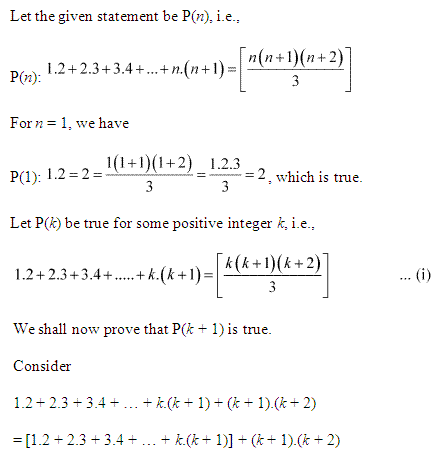
= k(k+1)(k+2)3 + (k + 1) (k + 2)

= (k + 1) (k + 2) + (k3 + 1)

= (k+1)(k+2)(k+3)3

= (k+1)(k+1+1)(k+1+2)3
Thus, P(k+1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Ex 4.1 Class 11 Maths Question 7:

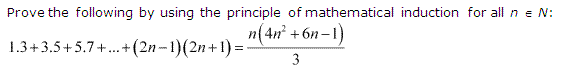
Ans :

Let the given statement be P(n), i.e.,
P(n) : 1 . 3 + 3 . 5 + 5 . 7 + … + (2n – 1) (2n + 1) = n(4n2+6n−1)3
For n = 1, we have
P(1) : 1 . 3 = 3
= 1(4.12+6.1−1)3=4+6−13=93 = 3, which is true.

Let P(k) be true for some positive integer k, Le.,
1 . 3 + 3 . 5 + 5 . 7 + ………………. + (2k – 1) (2k + 1) = k(4k2+6k−1)3 ……………(i)
We shall now prove that P(k + 1) is true.
Consider (1 . 3 + 3 . 5 + 5 . 7 + … + (2k – 1) (2k + 1) +{2 (k + 1) – 1} {2(k + 1) + 1}

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, .statement P(n) is true for all natural numbers i.e., n.

Ex 4.1 Class 11 Maths Question 8:

Ans :

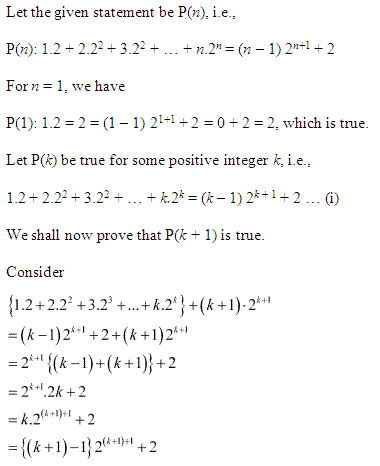
Ex 4.1 Class 11 Maths Question 9:

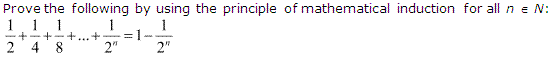
Ans :

Let the given statement be P(n), i.e.,

P(n) : 12+14+18+…+12n=1−12n

For n = 1, we have
P(1) : 12
= 1 – 121
= 12, which is true.

Let P(k) be true for some positive integer k, i.e.,
12+14+18+…+12k=1−12k

We shall now prove that P(k + 1) is true.
Consider (12+14+18+…+12k)+12k+1

= (1−12k)+12k+1

= 1−12k+122k=1−12k(1−12)

= 1−12k(12)=1−12k+1

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Ex 4.1 Class 11 Maths Question 10:

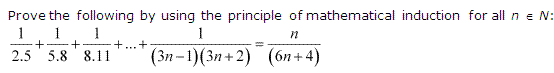
Ans :

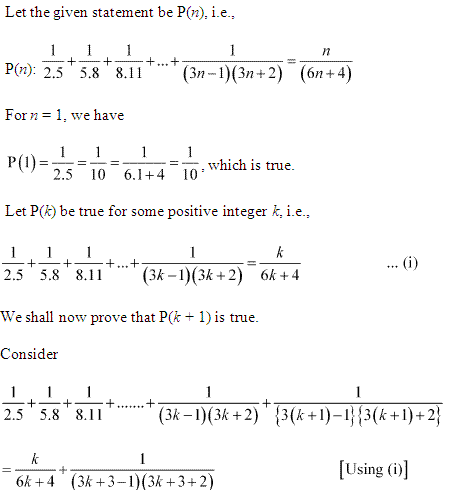
Ex 4.1 Class 11 Maths Question 11:

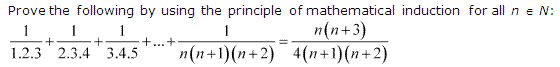
Ans :

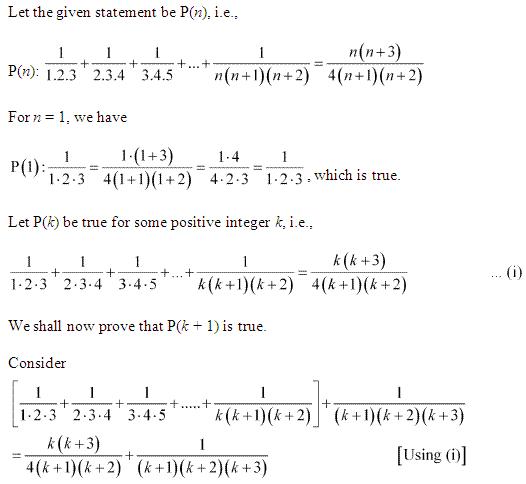
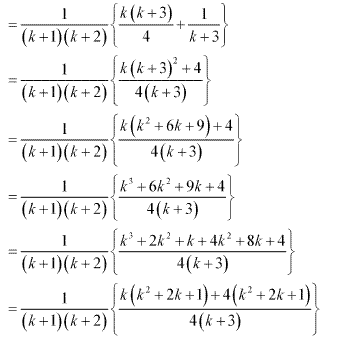
Ex 4.1 Class 11 Maths Question 12:

Ans :

Let the given statement be P(n), i.e.,

P(n) : a + ar + ar² + …………… + ar^{n – 1} = a(rn−1)r−1

For n = 1, we have

P(1) : a = a(r1−1)(r−1) = a, which is true.

Let P(k) be true for some positive integer k, i.e.,

a + ar + ar² + …………… + ar^{k – 1} = a(rk−1)r−1 …………..(i)

We shall now prove that P(k + 1) is true.
Consider
a + ar + ar² + …………… + ar^{k – 1}} + ar^{(k + 1) – 1} = a(rk−1)r−1 + ar^k [Using eQuestion (i)]

= a(rk−1)+ark(k−1)r−1

= a(rk−1)+ark+1−arkr−1

= ark−a+ark+1−arkr−1=ark+1−ar−1

= a(rk+1−1)r−1

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Ex 4.1 Class 11 Maths Question 13:

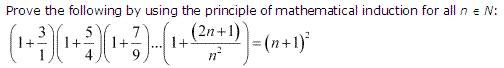
Ans :

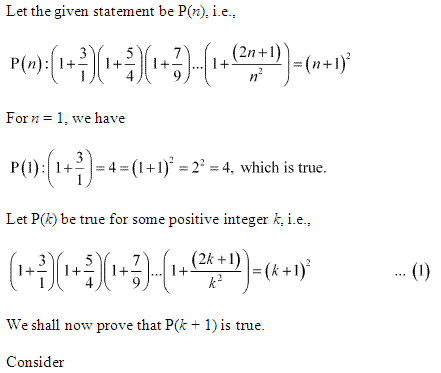
Ex 4.1 Class 11 Maths Question 14:

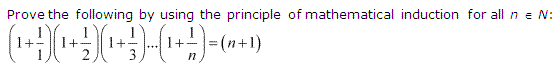
Ans :

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Ex 4.1 Class 11 Maths Question 15:
Prove the following by using the principle of mathematical indcution for all n ∈ N:
1² + 3² + 5² + … + (2n – 1)² = n(2n−1)(2n+1)3
Ans :

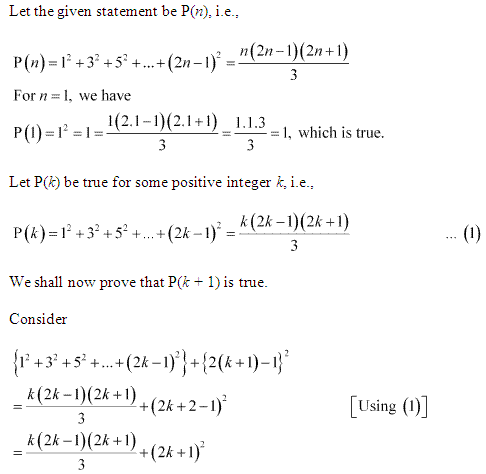
Ex 4.1 Class 11 Maths Question 16:

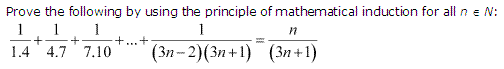
Ans :

Ex 4.1 Class 11 Maths Question 17:

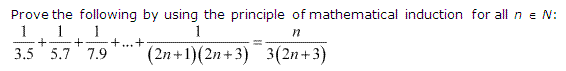
Ans :

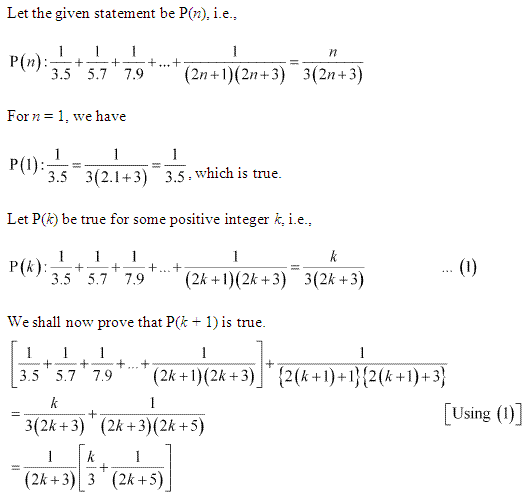
Ex 4.1 Class 11 Maths Question 18:

Ans :

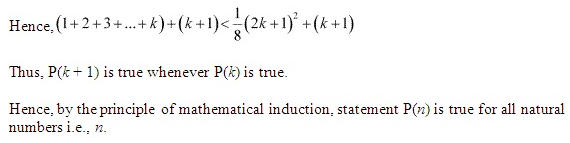
Ex 4.1 Class 11 Maths Question 19:

Ans :
Let the given statement be P(n), i.e.,
P(n) : n (n + 1) (n + 5) which is a multiple of 3.
It can be noted that P(n) is true for n=l since 1 (1 + 1) (1 + 5) = 12, which is a multiple of 3.
Let P(k) be true for some positive integer k, i.e., k (k + 1) (k + 5) is a multiple of 3.
∴ k (k + 1) (k + 5) = 3m, where m ∈ N ……………….(i)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider (k + 1) {(k +1 ) + 1} {(k + 1) + 5}
= (k + 1) (k + 2) {(k + 5) + 1}
= (k + 1) (k + 2) (k + 5) + (k + 1) (k + 2)
= {k (k + 1) (k + 5) + 2 (k + 1) (k + 5)} + (k +1) (k + 2)
= 3m + (k + 1) {2 (k + 5) + (k + 2)}
= 3m + (k + 1) {2k +10 + k + 2}
= 3m + (k + 1) (3k + 12)
= 3m + 3 (k + 1) (k + 4)
= 3 {m + (k + 1) (k + 4)}
= 3 × q, where, q = {m + (k +1) (k + 4)} is some natural number.
Therefore, (k +1) {(k +1) +1} {(k +1) + 5} is a multiple of 3.
Thus, P(k + 1) is trtie whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Ex 4.1 Class 11 Maths Question 20:

Ans :

Ex 4.1 Class 11 Maths Question 21:

Ans :

Ex 4.1 Class 11 Maths Question 22:

Ans :

Ex 4.1 Class 11 Maths Question 23:

Ans :

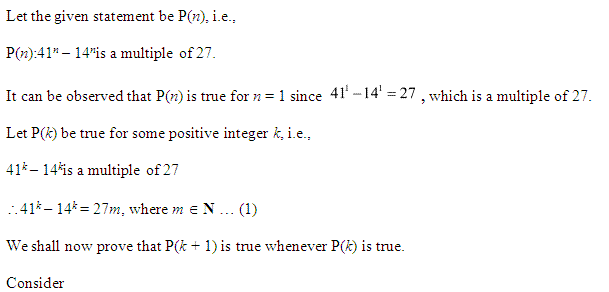
Ex 4.1 Class 11 Maths Question 24:

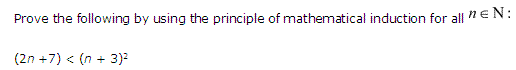
Ans :

Prove the following through the principle of mathematical induction for all values of n, where n is a natural number.

1) 1+3+3²+….+3^n-1=\(\frac { { (3 }^{ n }-1) }{ 2 } \)

2: 1³+2³+3³+……+n³ = (n(n+1)2)2

3: 1+11+2+11+2+3+……+11+2+3+…+n=2nn+1

4: 1.2.3+2.3.4+…+n(n+1)(n+2)= \(\frac { n(n+1)(n+2)(n+3) }{ 4 } \)

5: 1.3+2.32+3.33+…+n.3n

NCERT Solutions for Class 11 Maths Chapter 4 Principle of Mathematical Induction Hindi medium Ex 4.1