CBSE Class 10 Maths Notes Chapter 11 Constructions Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 11 Constructions. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

CBSE Class 10 Maths Notes Chapter 11 Constructions

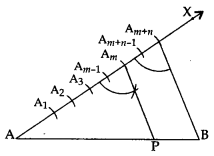
Determining a Point Dividing a given Line Segment, Internally in the given Ratio M : N

Let AB be the given line segment of length x cm. We are required to determine a point P by dividing it internally in the ratio m : n.

Steps of Construction:

• Draw a line segment AB = x cm.
• Make an acute ∠BAX at the end A of AB.
• Use a compass of any radius and mark off arcs. Take (m + n) points A₁, A₂, … A_m, A_m+1, …, A_m+n along AX such that AA₁ = A₁A₂ = … = A_m+n-1 , A_m+n
• Join A_m+nB.
• Passing through A_m, draw a line A_mP || A_m+nB to intersect AB at P. The point P so obtained is the A required point which divides AB internally in the ratio m : n.
  

Construction of a Tangent at a Point on a Circle to the Circle when its Centre is Known

Steps of Construction:

• Draw a circle with centre O of the given radius.
  
• Take a given point P on the circle.
• Join OP.
  
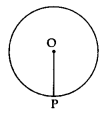
• Construct ∠OPT = 90°.
  
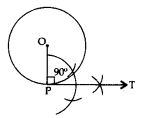
• Produce TP to T’ to get TPT’ as the required tangent.
  

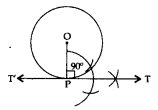
Construction of a Tangent at a Point on a Circle to the Circle when its Centre is not Known

If the centre of the circle is not known, then we first find the centre of the circle by drawing two non-parallel chords of the circle. The point of intersection of perpendicular bisectors of these chords gives the centre of the circle. Then we can proceed as above.

Construction of a Tangents from an External Point to a Circle when its Centre is Known

Steps of Construction:

• Draw a circle with centre O.
• Join the centre O to the given external point P.
• Draw a right bisector of OP to intersect OP at Q.
• Taking Q as the centre and OQ = PQ as radius, draw a circle to intersect the given circle at T and T’.
• Join PT and PT’ to get the required tangents as PT and PT’.
  

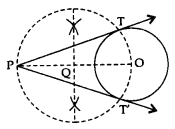
Construction of a Tangents from an External Point to a Circle when its Centre is not Known

If the centre of the circle is not known, then we first find the centre of the circle by drawing two non-parallel chords of a circle. The point of intersection of perpendicular bisectors of the chords gives the centre of the circle. Then we can proceed as above.

Construction of a Triangle Similar to a given Triangle as per given Scale Factor mn , m < n.

Let ΔABC be the given triangle. To construct a ΔA’B’C’ such that each of its sides is mn (m < n) of the corresponding sides of ΔABC.

Steps of Construction:

• Construct a triangle ABC by using the given data.
• Make an acute angle ∠BAX, below the base AB.
• Along AX, mark n points A₁, A₂ …, A_n, such that AA₁ = A₁A₂ = … = A_m-1 A_m = … A_n-1 A_n.
• Join A_nB.
• From A_m, draw A_mB’ parallel to AnB, meeting AB at B’.
• From B’, draw B’C’ parallel to BC, meeting AC at C’.
  Triangle AB’C’ is the required triangle, each of whose sides is mn (m < n) of the corresponding sides of ΔABC.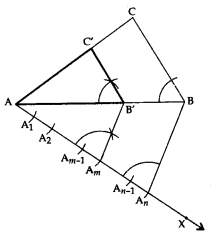

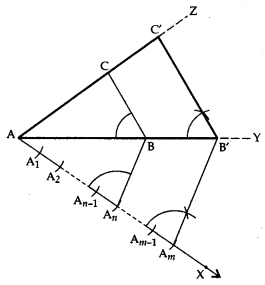
Construction of a Triangle Similar to a given Triangle as per given Scale Factor mn , m > n.

Let ΔABC be the given triangle and we want to construct a ΔAB’C’, such that each of its sides is mn (m > n) of the corresponding side of ΔABC.

Steps of Construction:

• Construct a ΔABC by using the given data.
• Make an acute angle ∠BAX, below the base AB. Extend AB to AY and AC to AZ.
• Along AX, mark m points A₁, A₂ …, A_n, ..A_m, such that AA₁ = A₁A₂ = A₂A₃ = … = A_n-1 A_n = … = A_m-1 A_m
• Join A_nB.
• From A_m, draw A_mB’ parallel to A_nB, meeting AY produced at B’.
• From B’, draw B’C’ parallel to BC, meeting AZ produced at C’.
• Triangle AB’C’ is the required triangle, each of whose sides is (mn) (m > n) of the corresponding sides of ΔABC.