Quadratic Equations Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
Find the roots of the equation x2 – 3x – m (m + 3) = 0, where m is a constant. (2011OD)
Solution:
x² – 3x – m(m + 3) = 0
D = b² – 4ac
D = (- 3)² – 4(1) [-m(m + 3)]
= 9 + 4m (m + 3)
= 4m² + 12m + 9 = (2m + 3)²

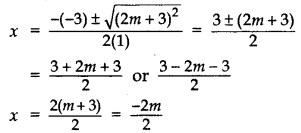
∴ x = m + 3 or -m

Question 2.
If 1 is a root of the equations ay² + ay + 3 = 0 and y² + y + b = 0, then find the value of ab. (2012D)
Solution:
ay² + ay + 3 = 0
a(1)² + a(1) + 3 = 0
2a = -3
a = −32

y² + y + b = 0
1² + 1 + b = 0
b = -2
∴ ab =(−32)(−2) = 3

Question 3.
If x = – 12 , is a solution of the quadratic equation 3x² + 2kx – 3 = 0, find the value of k. (2015D)
Solution:
The given quadratic equation can be written as, 3x² + 2kx – 3 = 0

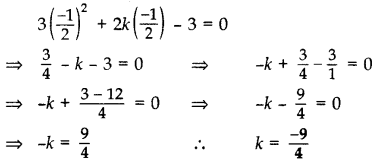
Question 4.
If the quadratic equation px\frac{1}{2} – 25–√ px + 15 = 0 has two equal roots, then find the value of p. (2015OD)
Solution:
The given quadratic equation can be written as px\frac{1}{2} – 25–√ px + 15 = 0
Here a = p, b = – 25–√ p, c = 15
For equal roots, D = 0
D = b² – 4ac – 0 …[∵ Equal roots
0 = (-25–√p)² – 4 × p × 15
0 = 4 × 5p² – 60p
0 = 20p² – 60p => 20p² = 60p
p = 60p20p = 3 ∴ p = 3

Quadratic Equations Class 10 Important Questions Short Answer-I (2 Marks)

Question 5.
Find the value of p so that the quadratic equation px(x – 3) + 9 = 0 has two equal roots. (2011D, 2014OD)
Solution:
We have, px (x – 3) + 9 = 0
px² – 3px + 9 = 0 Here a = p, b = -3p,
D = 0
b² – 4ac = 0 ⇒ (-3p)² – 4(p)(9) = 0
⇒ 9p² – 36p = 0
⇒ 9p (p – 4) = 0
⇒ 9p = 0 or p – 4= 0
p = 0 (rejected) or p = 4
∴ p = 4 ……..(∵ Coeff. of x² cannot be zero

Question 6.
Find the roots of 4x² + 3x + 5 = 0 by the method of completing the squares. (2011D)
Solution:
Here 4x² + 3x + 5 = 0


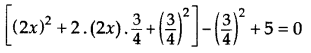
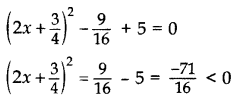
But (2x+34)2 cannot be negative for any real value of x.

Question 7.
Find the value of m so that the quadratic equation mx (x – 7) + 49 = 0 has two equal roots. (2011OD)
Solution:
We have, mx (x – 7) + 49 = 0
mx² – 7mx + 49 = 0
Here, a = m, b = – 7m, c = 49
D = b² – 4ac = 0 …[For equal roots
⇒ (-7m)² – 4(m) (49) = 0
⇒ 49m² – 4m (49) = 0
⇒ 49m (m – 4) = 0
⇒ 49m = 0 or m – 4 = 0
m = 0 (rejected) or m = 4
∴ m = 4

Question 8.
Solve for x:
36x² – 12ax + (a² – b²) = 0 (2011OD)
Solution:
We have, 36x² – 12ax + (a² – b²) = 0
⇒ (36x² – 12ax + a²) – b² = 0
⇒ [(6x)² – 2(6x)(a) + (a)²] – b² = 0
⇒ (6x – a)² – (b)² = 0 …[∵ x² – 2xy + y² = (x – y)²
⇒ (6x – a + b) (6x – a – b) = 0 „[∵ x² – y² = (x + y)(x – y)
⇒ 6x – a + b = 0 or 6x – a – b = 0
⇒ 6x = a – b or 6x = a + b
⇒ x = a−b6 or a+b6

Question 9.
Find the value(s) of k so that the quadratic equation x² – 4kx + k = 0 has equal roots. (2012D)
Solution:
We have, x² – 4kx + k = 0
Here a = 1, b = -4k:, c = k D = 0 …[Since, Equal roots
As b² – 4ac = 0
⇒ (-4k)² – 4(1) (k) = 0
⇒ 16k² – 4k = 0 ⇒ 4k(4k – 1) = 0
⇒ 4k = 0 or 4k – 1 = 0
k = 0 (rejected) or 4k = 1
∴ k = 1/4

Question 10.
Find the value of k for which the equation x² + k(2x + k – 1) + 2 = 0 has real and equal roots. (2017D)
Solution:
We have, x² + k(2x + k – 1) + 2 = 0
x² + 2kx + k² – k + 2 = 0
Here a = 1, b = 2k, c = k² – k + 2
D = 0 …[real and equal roots
∴ b² – 4ac = 0
⇒ (2k)² – 4 × 1(k² – k + 2) = 0
⇒ 4k² – 4 (k² – k + 2) = 0
⇒ 4(k² – k² + k – 2) = 0 ⇒ 4(k – 2) = 0
⇒ k – 2 = 0 ⇒ k = 2

Question 11.
Find the value of p for which the roots of the equation px(x – 2) + 6 = 0, are equal. (2012OD)
Solution:
We have , px(x – 2) + 6 = 0
px² – 2px + 6 = 0, p ≠ 0
Two equal roots …[Given
b² – 4ac = 0 ….[a = p, b = -2p, c = 6
∴ (-2p)² – 4(p)(6) = 0
4p² – 24p = 0 ⇒ 4p(p – 6) = 0
4p = 0 or p – 6 = 0
p = 0 (rejected) or p = 6
Since p cannot be equal to 0.
…[Standard form of a quad. eq. ax² + bx + c = 0, a ≠ 0
∴ P = 6

Question 12.
Solve the following quadratic equation for x: 43–√x² + 5x – 23–√ = 0 (2013D)
Solution:
43–√x² + 5x – 23–√ = 0
43–√x² + 8x – 3x – 23–√ =0
4x(3–√x + 2) – 3–√(3–√x + 2) = 0
(3–√x + 2)(4x – 3–√) = 0
3–√x + 2 = 0 or 4x – 3–√ = 0

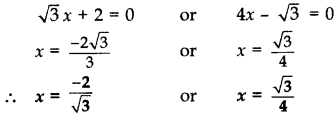
Question 13.
Solve the following for x: 2–√x² + 7x + 52–√ = 0 (2017D )
Solution:
2–√x² + 7x + 52–√ = 0
⇒ 2–√x² + 5x + 2x + 52–√ = 0
x(2–√x + 5) + 2–√(2–√x + 5) = 0
(2–√x + 5)(x + 2–√) = 0

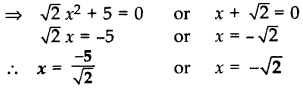
Question 14.
Solve the quadratic equation 2x² + ax – a² = 0 for x. (2014D)
Solution:
We have, 2x² + ax – a² = 0
2x² + 2ax – ax – a² = 0
2x(x + a) – a(x + a) = 0
(x + a) (2x – a) = 0
x + a = 0 or 2x – a = 0
∴ x = -a or x = a2
Alternatively:
First calculate D = b² – 4ac
Then apply x = −b±D√2a
We get x = -a, x = a2

Question 15.
Find the values of p for which the quadratic equation 4x² + px + 3 = 0 has equal roots. (2014OD)
Solution:
Given: 4x² + px + 3 = 0
Here a = 4, b = p. (= 3 … [Equal roots
D = 0 (Equal roots)
As b² – 4ac = 0
∴ (p)² – 4(4)(3) = 0
= p² – 48 = 0 ⇒ p² = 48
∴ p = ±16×3−−−−−√=±43–√

Question 16.
Solve the following quadratic equation for x: 4x²– 4a²x + (a⁴ – b⁴) = 0. (2015D)
Solution:
The given quadratic equation can be written as,
4x² – 4a²x + (a4⁴ – b⁴) = 0
(4x² – 4a²x + a⁴) – b⁴ = 0
or (2x – a²)² – (b²)² = 0
⇒ (2x – a² + b²) (2x – a² – b²) = 0
⇒ (2x – a² + b²) = 0 or (2x – a² – b²) = 0
∴ x = a2−b22 or x = a2+b22

Question 17.
Solve the following quadratic equation for x: 9x² – 6b²x – (a⁴ – b⁴) = 0 (2015D)
Solution:
The given quadratic equation can be written as
(9x² – 6b²x + b⁴) – a⁴ = 0
⇒ (3x – b²)² – (a²)² = 0
⇒ (3x – b² + a²) (3x – b² – a²) = 0 …[:: x² – y² = (x + y) (x – y)
⇒ 3x – b² + a² = 0 or 3x – b² – a² = 0
⇒ 3x = b² – a² or 3x = b² + a²

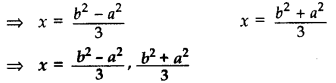
Question 18.
Solve the following quadratic equation for x: 4x² + 4bx – (a² – b²) = 0 (20150D)
Solution: The given quadratic equation can be written as
4x² + 4bx + b² – a²2 = 0
⇒ (2x + b)² – (a)² = 0
⇒ (2x + b + a) (2x + b – a) = 0 …[x² – y² = (x + y)(x – y)
⇒ (2x + b + a) = 0 or (2x + b – a) = 0
⇒ 2x = -(a + b) or 2x = (a – b)

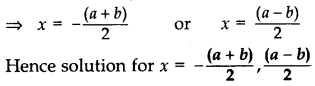
Question 19.
Solve the following quadratic equation for x: x² – 2ax – (4b² – a²) = 0) (2015OD)
Solution:
Given quadratic equation can be written as
x² – 2ax – 4b² + a² = 0.
(x² – 2ax + a²) – 4b² = 0 or (x – a)² – (2b)² = 0
As we know,
[a² – b² = (a + b)(a – b)]
∴ (x – a + 2b) (x – a – 2b) = 0
⇒ x – a + 2b = 0 or x – a – 2b = 0
⇒ x = a – 2b or x = a + 2b
⇒ x = a – 2b and x = a + 2b

Question 20.
If x = 23 and x = -3 are roots of the quadratic equation ax² + 7x + b = 0, find the values of a and b. (2016D)
Solution:
We have, ax² + 7x + b = 0
Here ‘a’ = a, ‘b’ = 7, ‘c’ = b
Now, α = 23 and β = -3 … [Given

Question 21.
Find the value of p, for which one root of the quadratic equation px² – 14x + 8 = 0 is 6 times the other. (20170D)
Solution:
Given equation is px² – 14x + 8 = 0.
Here a = p b = -14 c = 8
Let roots be a and 6α.

Question 22.
If -5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, find the value of k. (2016OD)
Solution:
We have, 2x² + px – 15 =0
Since (-5) is a root of the given equation
∴ 2(-5)² + p(-5) – 15 = 0
⇒ 2(25) – 5p – 15 = 0
⇒ 50 – 15 = 5p
⇒ 35 = 5p ⇒ p = 7 …(i)
Now, p(x² + x) + k ⇒ px² + px + k = 0
7x² + 7x + k = 0 …[From (i)
Here, a = 7, b = 7, c = k
D = 0 …[Roots are equal
b² – 4ac = 0
⇒ (7)² – 4(7)k = 0 ⇒ 49 – 28k = 0
⇒ 49 = 28k ∴ k = 4928=74

Question 23.
Solve for x: 2x+9−−−−−√ + x = 13. (20160D)
Solution:
2x+9−−−−−√ + x = 13 …(i)
⇒ 2x+9−−−−−√ = 13 – x
⇒ (2x+9−−−−−√)² = (13 – x)² …[Squaring both sides
⇒ 2x + 9 = 169 + x²2 – 26x
⇒ 0 = 169 + x²2 – 26x – 2x – 9
⇒ x² – 28x + 160 = 0
⇒ x² – 20x – 8x + 160 = 0
⇒ x(x – 20) – 8(x – 20) = 0
⇒ (x – 20) (x – 8) = 0
⇒ x – 8 = 0 or x – 20 = 0
⇒ x = 8 or x = 20
Checking, When x = 8 in (i)
2(8)+9−−−−−−−√ + 8 = 13
25−−√ + 8 = 13
5 + 8 = 13 ⇒ 13 = 13 …[True
∴ x = 8 is the solution.
Checking, When x = 20 in (i),
2(20)+9−−−−−−−√ + 20 = 13 … [From (1)
49−−√ + 20 = 13
7 + 20 ≠ 13 …[False
∴ x = 20 is not a solution.
Therefore, x = 8 is the only solution.

Question 24.
Solve for x: 6x+7−−−−−√ – (2x – 7) = 0 (20160D)
Solution:
6x+7−−−−−√ – (2x – 7) = 0…(i)
⇒ 6x+7−−−−−√ = 2x – 7
⇒ (6x+7−−−−−√)² = (2x – 7)² …[Squaring both sides
⇒ 6x + 7 = 4x² – 28x + 49
⇒ 0 = 4x² – 28x – 6x – 7 + 49
⇒ 4x² – 34x + 42 = 0
⇒ 2x² – 17x + 21 = 0 …[Dividing by 2
⇒ 2x² – 14x – 3x + 21 = 1
⇒ 2x(x – 7) – 3(x – 7) = 0
⇒ (x – 7) (2x – 3) = 0
⇒ x – 7 = 0 or 2x – 3 = 0 =
x= 7 or x = 32
Checking: When x = 7 in (i),
6(7)+7−−−−−−−√ – [2(7) – 7] = 0
49−−√ – (14 – 7) = 0
7 – 7 = 0 … [True
Checking: When x = 32 in (i),
6(32)+7−−−−−−−−√−(2(32)−7) = 0
9+7−−−−√ – (3 – 7) = 0
16−−√ – (-4) = 0
4 + 4 ≠ 0
∴ x = 7 is the only solution.

Quadratic Equations Class 10 Important Questions Short Answer-II (3 Marks)

Question 25.
ind the roots of the following quadratic equation: 23–√x² – 5x + 3–√ = 0 (2011D)
Solution:
We have, 23–√x² – 5x + 3–√ = 0
Here, a = 23–√, h = -5, c = 3–√
D = b² – 4ac
∴ D = (-5)² – 4 (23–√)(3–√)
= 25 – 24 = 1

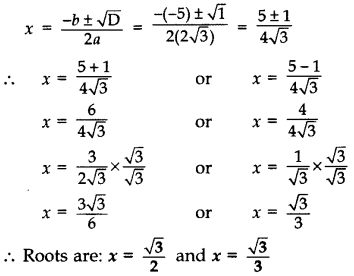
Question 26.
Solve for x: 4x² – 4ax + (a² – b²) = 0 (2011OD)
Solution:
4x² – 4ax + (a² – b²) = 0
⇒ [4x² – 4ax + a²] – b² = 0
⇒ [(2x)² – 2(2x)(a) + (a)²] – b² = 0
⇒ (2x – a)² – (b)² = 0
⇒ (2x – a + b) (2x – a – b) = 0
⇒ 2x – a + b = 1 or 2x – a – b = 0
2x = a – b or 2x = a + b
∴ x = a−b2 or x = a+b2

Question 27.
Solve for x: 3x²} – 26–√ x + 2 = 0 (2012D)
Solution:
3x²} – 26–√ x + 2 = 0
⇒ 3x² – 6–√x – 6–√x + 2 = 0
⇒ 3–√x (3–√x – 2–√ – 2–√(3–√x – 2–√) = 0
⇒ (3–√x – 2–√)(3–√x – 2–√) = 0
⇒ 3–√x – 2–√ = 0 ⇒ x = 2√3√
∴ x = 6√3 ….[2√3√×3√3√=6√3

Question 28.
Find the value(s) of k so that the quadratic equation 2x² + kx + 3 = 0 has equal roots. (2012D)
Solution:
Given: 2x² + kx + 3 = 0
Here a = 2, b = k, c= 3
D = 0 … [Since roots are equal
As b² – 4ac = 0 ∴ K² – 4(2)(3) = 0
K² – 24 = 0 or k² = 24
∴ k = 2×2×6−−−−−−−√=±26–√

Question 29.
Find the value(s) of k so that the quadratic equation 3x² – 2kx + 12 = 0 has equal roots. (2012D)
Solution:
Given: 3x² – 2kx + 12 = 0
Here a = 3, b = -2k, c = 12
D = 0 … [Since roots are equal As
b² – 4ac = 0
∴ (-2k)² – 4(3) (12) = 0
⇒ 4k² – 144 = 0 ⇒ k² = 1444 = 36
∴ k = ±36−−√=±6

Question 30.
Solve the following quadratic equation for x: x² – 4ax – b² + 4a² = 0 (2012OD)
Solution:
We have, x² – 4ax – b² + 4a² = 0
⇒ x² – 4ax + 4a² – b\frac{144}{4} = 0
⇒ [(x)\frac{144}{4} – 2(x)(2a) + (2a)\frac{144}{4}] – (b)² = 0
(x – 2a)² – (b)² = 0
(x – 2a + b) (x – 2a – b) = 0
x – 2a + b = 0 or x – 2a – b = 0
∴ x = 2a – b or x = 2a + b

Question 31.
Find the value of k for which the roots of the equation kx(3x – 4) + 4 = 0, are equal. (20120D)
Solution:
We have, kx(3x – 4) + 4 = 0
3kx² – 4kx + 4 = 0
Here a = 3k, b = -4k, c = 4
D = 0 … [Since roots are equal
b² – 4ac = 0
∴ (-4k)² – 4(3k) (4) = 0
16k² – 48k = 0
16k (k – 3) = 0
16k = 0 or k – 3 = 0
k = 0 or k = 3
…[Rejecting k = 0, as coeff. of x² cannot be zero
∴ k = 3

Question 32.
Find the value of m for which the roots of the equation. mx (6x + 10) + 25 = 0, are equal. (2012OD)
Solution:
We have, mx(6x + 10) + 25 = 0
6mx² + 10mx + 25 = 0
Here a = 6m, b = 10m, c = 25
D = 0 … Since roots are equal
b² – 4ac = 0
∴ (10m)² – 4(6m) (25) = 0
100m² – 600m = 0 ⇒ 100m (m – 6) = 0
100m = 0 or m – 6 = 0
m = 0 or m = 6
…[Rejecting m = 0, as coeff. of x² cannot be zero
∴ m = 6

Question 33.
For what value of k, the roots of the quadratic equation kx(x – 25–√) + 10 = 0, are equal? (2013D)
Solution:
We have, kx(x – 25–√) + 10 = 0
kx² – 25–√kx + 10 = 0
Here a = k, b= -25–√k, c= 10
D = 0 …[∵ Roots are equal
As b² – 4ac = 0
∴ (-2 5–√k)² – 4(k)(10) = 0
20k² – 40k = 0
⇒ 20k(k – 2) = 0
∴ 20k = 0 or k – 2 = 0
k = 0 (rejected) or k = 2
…[∵ Coeff. of x² cannot be zero
∴ k= 2

Question 34.
For what values of k, the roots of the quadratic equation (k + 4)x² + (k + 1)x + 1 = 0 are equal? (2013D)
Solution:
We have, (k + 4) x² + (k + 1) x + 1 = 0
Here, a = k + 4, b = k + 1, c = 1
D =0 …[∵ Roots are equal
b² – 4ac = 0
∴ (k + 1)² – 4(k + 4)(1) = 0
k² + 2k + 1 – 4k – 16 = 0
k² – 2k – 15 = 0
k² – 5k + 3k – 15 = 0
k(k – 5) + 3(k – 5) = 0
(k – 5)(k + 3) = 0
k – 5 = 0 or k + 3= 0
k = 5 or k = -3
∴ k = 5 and -3

Question 35.
For what value of k, are the roots of the quadratic equation: (k – 12)x² + 2(k – 12)x + 2 = 0 equal? (2013OD)
Solution:
We have, (k – 12)x² + 2(k – 12)x + 2 = 0
The given quadratic equation will have equal roots if D = 0 ⇒ b² – 4ac = 0
Here a = (k – 12), b = 2(k – 12), c = 2
b² – 4ac = 0
0 = 4(k – 12)² – 4 × (k – 12) × 2
0 = (k – 12)[4(k – 12) – 4 × 2]
0 = (k – 12) 4[k – 12 – 2]
0 = 4(k – 12) (k – 14)
∴ 4(k – 12)(k – 14) = 0
∴ k = 12 (rejected) or k = 14
But k cannot be equal to 12 because in that case the given equation will imply 2 = 0 which is not true.
∴ k = 14

Question 36.
For what value of k, are the roots of the quadratic equation y² + k² = 2 (k + 1)y equal? (2013OD)
Solution:
y² + k² = 2(k + 1)y
y² – 2(k + 1)y + k² = 0
Here a = 1, b = -2(k + 1), c = k²
D = 0 … [Roots are equal
b² – 4ac = 0
∴ [-2(k + 1)]² – 4 × (1) × (k²) = 0
⇒ 4(k² + 2k + 1) – 4k² = 0
⇒ 4k² + 8k + 4 – 4k² = 0
⇒ 8k + 4 = 0
⇒ 8k = -4 ∴ k = −48=−12

Question 37.
Find that non-zero value of k, for which the quadratic equation kx² + 1 – 2(k – 1)x + x² = 0 has equal roots. Hence find the roots of the equation. (2015D)
Solution:
The given quadratic equation can be written as
kx² + x² – 2(k – 1)x + 1 = 0
(k + 1) x² – 2 (k – 1) x + 1 = 0 …(i)
Here, a = (k + 1), b = -2(k – 1), c = 1
For equal roots, D = 0
D = b² – 4ac
⇒ (-2(k – 1)]² – 4 × (k + 1) × 1 = 0
⇒ 4(k − 1)² – 4(k + 1) = 0
⇒ 4k² + 4 – 8k – 4k – 4 = 0
⇒ 4k² – 12k = 0 ⇒ 4k(k – 3) = 0
k = 3 or k = 0 (rejected)
∴ k = 3
Putting k = 3 put in equation (i), we get
⇒ 4x² – 4x + 1 = 0
⇒ 4x² – 2x – 2x + 1 = 0
⇒ 2x(2x – 1) – 1(2x – 1) = 0
⇒ (2x – 1) (2x – 1) = 0
⇒ 2x – 1 = 0 or 2x – 1 = 0
⇒ x = 12 or x = 12
Roots are 12 and 12

Question 38.
Find that value of p for which the quadratic equation (p + 1)x² – 6(p + 1)x + 3 (p + 9) = 0, p ≠ -1 had equal roots. (2015D(
Solution:
For the given quadratic equation to have equal roots, D = 0
Here a = (p + 1), b = -6(p + 1), c = 3(p + 9)
D = b² – 4ac
⇒ [-6(p + 1)]² – 4(p + 1).3 (p + 9) = 0
⇒ 36(p + 1)² – 12(p + 1) (p + 9) = 0
⇒ 12(p + 1) (3p + 3 – p – 9) = 0
⇒ 12(p + 1)(2p – 6) = 0
⇒ 24(p + 1)(p – 3) = 0
⇒ p + 1 = 0 or p – 3 = 0
⇒ p = -1 (rejected) or p = 3
∴ p = 3

Question 39.
Solve for x: 3–√x² – 223−−√x – 23–√ = 0 (2015OD)
Solution:
The given quadratic equation can be written as
3–√x² – 223−−√x – 23–√ = 0
Here, a = 3–√, b = -22–√, c= -23–√
D = b² – 4ac

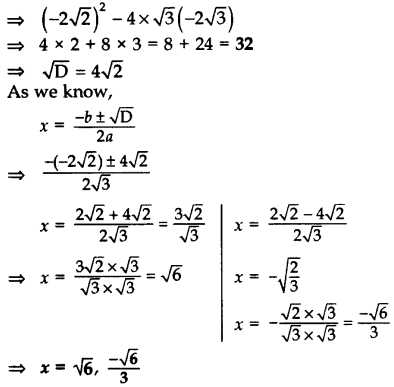
Question 40.
Solve for x: 2x² + 63–√x – 60 = 0 (2015OD)
Solution:
Given equation can be written as
2(x² + 33–√ x – 30) = 0
x² + 33–√ x – 30 = 0
Here, a = 1, b = 33–√, C = -30
D = b² – 4ac

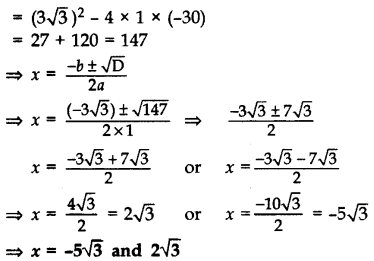
Question 41.
If the roots of the quadratic equation (a – b)x² + (b – c)x + (c – a) = 0 are equal, prove that 2a = b + c. (2016OD)
Solution:
Here’a’ = a – b, ‘b’ = b – c, ‘c’ = c – a
D = 0 ….[Roots are equal
b² – 4ac = 0
⇒ (b – c)² – 4(a – b)(c – a) = 0
⇒ b² + c² – 2bc – 4(ac – a² – bc + ab) = 0
⇒ b² + c² – 2bc – 4ac + 4a² + 4bc – 4ab = 0
⇒ 4a² + b2² + c² – 4ab + 2bc – 4ac = 0
⇒ (-2a)² + (b)² + (c)2² + 2(-2a)(b) + 2(b)(c) + 2(c)(-2a) = 0
⇒ [(-2a) + (b) + (c)]² = 0
….[∵ x² + y² + z² + 2xy + 2yz + 2zx = (x + y + z)²
Taking square-root on both sides
-2a + b + c = 0
⇒ b + c = 2a ∴ 2a = b + c

Question 42.
Solve the equation 4x−3=52x+3;x≠0,−32, for x. (2014D)
Solution:

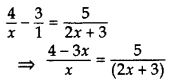
⇒ 5x = (2x + 3) (4 – 3x)
⇒ 5x = 8x – 6x² + 12 – 9x
⇒ 5x – 8x + 6x² – 12 + 9x = 0
⇒ 6x² + 6x – 12 = 0
⇒ x² + x – 2 = 0 …[Dividing by 6
⇒ x² + 2x – x – 2 = 0
⇒ x(x + 2) – 1(x + 2) = 0
⇒ x – 1 = 0 or x + 2 = 0
∴ x = 1 or x = -2

Question 43.
Solve the equation 3x+1−12=23x−1; x ≠ -1, x ≠ 13 for x. (2014D)
Solution:

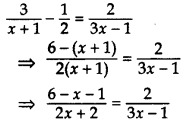
⇒ 2(2x + 2) = (5 – x)(3x – 1)
⇒ 4x + 4 = 15x – 5 – 3x² + x
⇒ 4x + 4 – 15x + 5 + 3x² – x = 0
⇒ 3x² – 12x + 9 = 0
⇒ x² – 4x + 3 = 0 …[Dividing by 3
⇒ x² – 3x – x + 3 = 0
⇒ x(x – 3) – 1(x – 3) = 0
⇒ (x – 1) (x – 3) = 0
⇒ x – 1 = 0 or x – 3 = 0
∴ x = 1 or x = 3

Question 44.
Solve the equation 14x+3−1=5x+1; x ≠ -3, -1, for x. (2014D)
Solution:

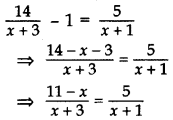
⇒ 5(x + 3) = (11 – x) (x + 1)
⇒ 5x + 15 = 11x + 11 – x² – x
⇒ 5x + 15 – 11x – 11 + x² + x = 0
⇒ x² – 5x + 4 = 0
⇒ x² – 4x – x + 4 = 0
⇒ x(x – 4) – 1(x – 4) = 0
⇒ (x – 1) (x – 4) = 0
⇒ x – 1=0 or x – 4 = 0
⇒ x= 1 or x = 4

Question 45.
Solve for x: 2xx−3+12x+3+3x+9(x−3)(2x+3) = 0, x ≠ 3, −32
Solution:

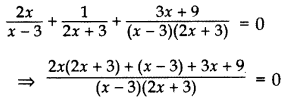
⇒ 4x² + 6x + x – 3 + 3x + 9 = 0
⇒ 4x² + 10x + 6 = 0
⇒ 2x² + 5x + 3 = 0 …[Dividing both sides by 2
⇒ 2x² + 3x + 2x + 3 = 0
⇒ x(2x + 3) + 1(2x + 3) = 0
⇒ (2x + 3) (x + 1) = 0
⇒ 2x + 3 = 0 or x + 1 = 0
⇒ x= −32 or x = -1
But, x ≠ −322 …[Given
∴ x= -1 is the only solution.

Question 46.
Solve for x: x−1x−1+x−2x+2=4−2x+3x−2; x ≠1, -2, 2 (2016D)
Solution:

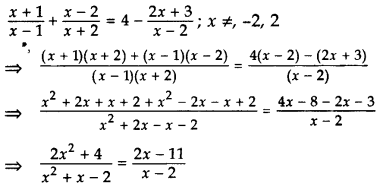
⇒ (2x² + 4)(x – 2) = (2x – 11)(x² + x – 2)
⇒ 2x³ – 4x² + 4x – 8 = 2x³ + 2x² – 4x – 11x² – 11x + 22
⇒ 2x³ – 4x² + 4x – 8 – 2x³ – 2x² + 4x + 11x² + 11x – 22 = 0
⇒ 5x² + 19x – 30 = 0
⇒ 5x² + 25x – 6x – 30 = 0
⇒ 5x(x + 5) – 6(x + 5) = 0
⇒ (x + 5) (5x – 6) = 0
⇒ x + 5 = 0 or 5x – 6 = 0
⇒ x = -5 or x = 65

Question 47.
Solve the following quadratic equation for x: x2+(aa+b+a+ba)x+1=0 (2016D)
Solution:

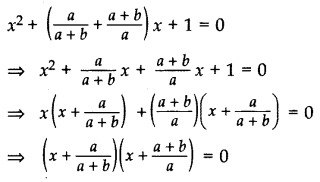
Question 48.
Solve for x: 1(x−1)(x−2)+1(x−2)(x−3)=23, x ≠ 1, 2, 3 (2016OD)
Solution:

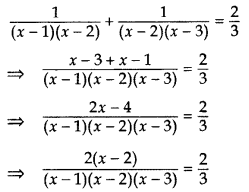
⇒ (x – 1)(x – 3) = 3
⇒ x² – 3x – x + 3 – 3 = 0
⇒ x² – 4x = 0 ⇒ x(x – 4) = 0
⇒ x = 0 or x – 4 = 0
∴ x = 0 or x = 4

Question 49.
Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Find the numbers. (2016OD)
Solution:
Let three consecutive natural numbers are x, x + 1, x + 2.
According to the question,
(x + 1)² – [(x + 2)² – x²] = 60
⇒ x² + 2x + 1 – (x² + 4x + 4 – x²) = 60
⇒ x² + 2x + 1 – 4x – 4 – 60 = 0
⇒ x² – 2x – 63 = 0
⇒ x² – 9x + 7x – 63 = 0
⇒ x(x – 9) + 7(x – 9) = 0
⇒ (x – 9) (x + 7) = 0
⇒ x – 9 = 0 or x + 7 = 0
⇒ x = 9 or x = -7
Natural nos. can not be -ve, ∴ x = 9
∴ Numbers are 9, 10, 11.

Question 50.
If the sum of two natural numbers is 8 and their product is 15, find the numbers. (2012OD)
Solution:
Let the numbers be x and (8 – x).
According to the Question,
x(8 – x) = 15
⇒ 8x – x² = 15
⇒ 0 = x² – 8x + 15
⇒ x² – 5x – 3x + 15 = 0
⇒ x(x – 5) – 3(x – 5) = 0
⇒ (x – 3)(x – 5) = 0
x – 3 = 0 or x – 5 = 0
x = 3 or x = 5
When x = 3, numbers are 3 and 5.
When x = 5, numbers are 5 and 3.

Quadratic Equations Class 10 Important Questions Long Answer (4 Marks)

Question 51.
Find the values of k for which the quadratic equation (3k + 1)x² + 2(k + 1)x + 1 = 0 has equal roots. Also find the roots. (2014D)
Solution:
(3k + 1)x² + 2(k + 1) + 1 = 0
Here, a = 3k + 1, b = 2(k + 1), c = 1
D = 0 …[∵ Roots are equal
As b² – 4ac = 0
∴ [2(k + 1)]² – 4(3k + 1)(1) = 0
4(k + 1)² – 4(3k + 1) = 0
4(k² + 2k + 1 – 3k – 1) = 0
(k² – k) = 04 ⇒ k(k – 1) = 0
k = 0 or k – 1 = 0
∴ k = 0 or k = 1
Roots are x = −b2a ..[As equal roots (Given)
x = −2(k+1)2(3k+1) ⇒ x = −(k+1)(3k+1)
When k = 0, x = −(0+1)0+1 = -1
∴ Equal roots are -1 and -1
When k = 1, x = −(1+1)3+1
x= −24=−12
∴ Equal roots are −12 and −12

Question 52.
Find the value of p for which the quadratic equation (2p + 1)x² – (7p + 2)x + (7p – 3) = 0 has equal roots. Also find these roots. (2014D)
Solution:
(2p + 1)x² – (7p + 2)x + (7p – 3) = 0
Here, a = 2p + 1, b = -(7p + 2), c = 7p – 3
D = 0 …[∵ Equal roots As h2 – 4ac = 0
∴ [-(7p + 2)]² – 4(2p + 1)(7p – 3) = 0
⇒ (7p + 2)² – 4(14p² – 6p + 7p – 3) = 0
⇒ 49p² + 28p + 4 – 56p² + 24p – 28p + 12 = 0
⇒ -7p² + 24p + 16 = 0
⇒ 7p² – 24p – 16 = 0 … [Dividing both sides by -1
⇒ 7p² – 28p + 4p – 16 = 0
⇒ 7p(p – 4) + 4(p – 4) = 0
⇒ (p – 4) (7p + 4) = 0
⇒ p – 4 = 0 or 7p + 4 = 0
⇒ p = 4 or p = −47


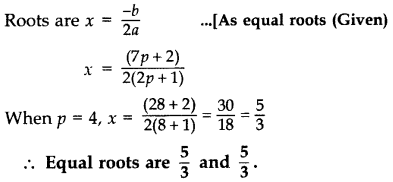
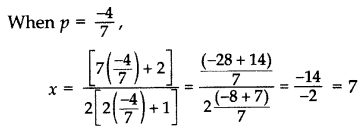
∴ Equal roots are 7 and 7.

Question 53.
Find the roots of the equation 1x+4−1x−7=1130, x ≠ -4, 7 (2011D)
Solution:

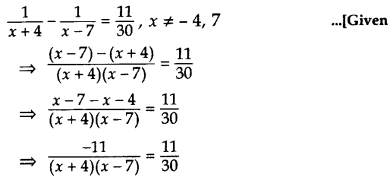
⇒ (x + 4)(x – 7) = – 30
⇒ x² – 7x + 4x – 28 + 30 = 0
⇒ x² – 3x + 2 = 0
⇒ x² – x – 2x + 2 = 0
⇒ x(x – 1) – 2(x – 1) = 0
⇒ (x – 1)(x – 2) = 0
⇒ x – 1 = 0 or x – 2 = 0
∴ x = 1 or x = 2

Question 54.
Find the roots of the equation: 12x−3+1x−5=1, x ≠ 32, 5. (2011OD)
Solution:

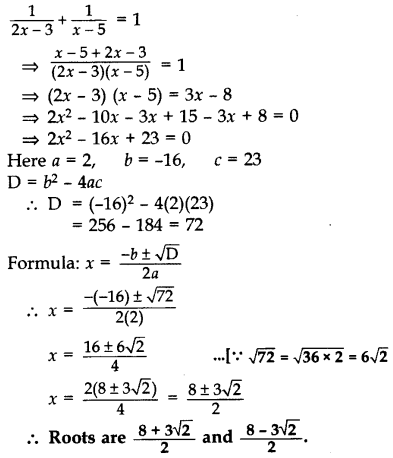
Question 55.
Solve for x:
1x−3+2x−2=8x; x ≠ 0, 2, 3 (2013OD)
Solution:


⇒ 8(x – 3)(x – 2) = x(3x – 8)
⇒ 8(x² – 3x – 2x +6) = 3x² – 8x
⇒ 8x² – 24x – 16x + 48 – 3x² + 8x = 0
⇒ 5x² – 32x + 48 = 0
⇒ 5x² – 20x – 12x + 48 = 0
⇒ 5x(x – 4) – 12(x – 4) = 0
⇒ (x – 4)(5x – 12) = 0
⇒ x – 4 = 0 or 5x – 12 = 0
x = 4 or x = 125

Question 56.
Solve for x: 4x−3=52x+3; x ≠ 0, −32 (2013OD)
Solution:

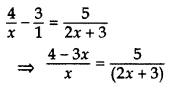
⇒ 5x = (2x + 3 (4 – 3x)
⇒ 5x = 8x – 6x² + 12 – 9x
⇒ 5x – 8x + 6x² – 12 + x = 0
⇒ 6x + 6x – 12 = 0
⇒ x² + x – 2 = 0 …[Dividing by 6
⇒ x² + 2x – x – 2 = 0
⇒ x(x + 2) – 1(x + 2) = 0
⇒ (x – 1)(x + 2) = 0
⇒ x – 1 = 0 or x + 2 = 0
∴ x = 1 or x = -2

Question 57.
Solve for x: x−2x−3+x−4x−5=103; x ≠ 3, 5 (2014OD)
Solution:

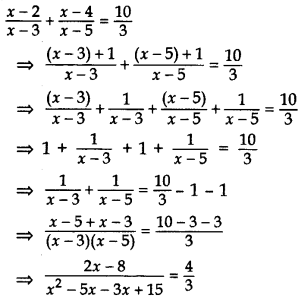
⇒ 4(x² – 8x + 15) = (6x – 24)
⇒ 4x² – 32x + 60 – 6x + 24 = 0
⇒ 4x² – 38x + 84 = 0
⇒ 2x² – 19x + 42 = 0 …[Dividing by 2
⇒ 2x² – 12x – 7x + 42 = 0
⇒ 2x(x -6) – 7(x – 6) = 0
⇒ (x – 6) (2x – 7) = 0
⇒ x – 6 = 0 or 2x – 7 = 0
∴ x = 6 or x = 72

Question 58.
Solve for x: 3x+1+4x−1=294x−1;x≠1,−1,14 (2015D)
Solution:

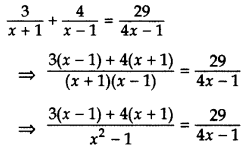
⇒ [3(x – 1) + 4(x + 1)] [4x – 1] = 29(x² – 1)
⇒ (3x – 3 + 4x + 4) [4x – 1] = 29(x² – 1)
⇒ (7x + 1) (4x – 1) = 29x² – 29
⇒ 28x² – 3x – 1 = 29x² – 29
⇒ x² + 3x – 28 = 0
⇒ x² + 7x – 4x – 28 = 0
⇒ x(x + 7) – 4(x + 7) = 0
⇒ (x + 7) (x – 4) = 0
x = -7 or x = 4
∴ x = -7 and 4

Question 59.
Solve for x: 2x+1+32(x−2)=235x,x≠0,−1,2 (2015D)
Solution:

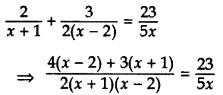
⇒ 5x[4 (x – 2) + 3x + 3) = 46(x + 1) (x – 2)
⇒ 5x[4x – 8 + 3x + 3) = 46[x² – 1x – 2]
⇒ 5x (7x – 5) = 46 (x² – x – 2)
⇒ 35x² – 25x = 46x² – 46x – 92
⇒ 35x² – 46x² – 25x + 46x + 92 = 0
⇒ 11x² – 21x – 92 = 0
Here, a = 11, b = -21, c = -92
D = b² – 4ac
= (-21)² – 4 × 11 × (-92)
= 441 + 4048 = 4489

Question 60.
Find x in terms of a, b and c: ax−a+bx−b=2cx−c, x ≠ a, b, c (2016D)
Solution:

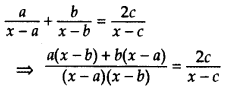
⇒ (x – c)[ax – ab + bx – ab] = 2c(x – a)(x – b)
⇒ (x – c)(ax + bx – 2ab) = 2c(x² – bx – ax + ab)
⇒ ax² + bx² – 2abx – acx – bcx + 2abc = 2cx² – 2bcx – 2cax + 2abc
⇒ ax² + bx² – 2abx – acx – bcx – 2cx² + 2bcx + 2cax = 0
⇒ ax² + bx² – 2cx² – 2abx + bcx + cax = 0
⇒ x²(a + b – 2c) + x(-2ab + bc + ca) = 0
⇒ x[x (a + b – 2c) + (-2ab + bc + ca)] = 0
⇒ x = 0 or x (a + b – 2c) + (-2ab + bc + ca) = 0
⇒ x = 0 or x (a + b – 2c) = 2ab – bc – ca = 0
∴ x = 2ab−bc−cda+b−2c

Question 61.
Solve the following for x:  (2013D)
Solution:

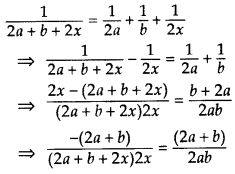
⇒ 2x² + 2ax + bx + ab = 0
⇒ 2x (x + a) + b(x + a) = 0
⇒ (x + a) (2x + b) = 0
⇒ x + a = 0 or 2x + b = 0
⇒ x = -a or x = −b2

Question 62.
A shopkeeper buys some books for 80. If he had bought 4 more books for the same amount, each book would have cost ₹1 less. Find the number of books he bought. (2012D)
Solution:
Let the number of books he bought = x
Increased number of books he had bought = x +4
Total amount = ₹80
According to the problem,

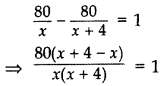
⇒ x(x + 4) = 320
⇒ x² + 4x – 320 = 0
⇒ x² + 20x – 16x – 320 = 0
⇒ x(x + 20) – 16(x + 20) = 0
⇒ (x + 20) (x – 16) = 0
⇒ x + 20 = 0 or x – 16 = 0
⇒ x = -20 … (neglected) or x = 16
∴ Number of books he bought = 16

Question 63.
Sum of the areas of two squares is 400 cm². If the difference of their perimeters is 16 cm, find the sides of the two squares. (2013D)
Solution:
Let the side of Large square = x cm
Let the side of small square = y cm
According to the Question,
x² + y² = 400… (i) …[∵ area of square = (side)²
4x – 4y = 16 …[∵ Perimeter of square = 4 sides
⇒ x – y = 4 … [Dividing both sides by 4
⇒ x = 4 + y …(ii)
Putting the value of x in equation (i),
(4 + y)² + y2² = 400
⇒ y² + 8y + 16 + y² – 400 = 0
⇒ 2y² + 8y – 384 = 0
⇒ y² + 4y – 192 = 0 … [Dividing both sides by 2
⇒ y² + 16y – 12y – 192 = 0
⇒ y(y + 16) – 12(y + 16) = 0
⇒ (y – 12)(y + 16) = 0
⇒ y – 12 = 0 or y + 16 = 0
⇒ y = 12 or y = -16 … [Neglecting negative value
∴ Side of small square = y = 12 cm
and Side of large square = x = 4 + 12 = 16 cm

Question 64.
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field. (2015OD)
Solution:
Let the length of shorter side be x m.
∴ length of diagonal = (x + 16) m
and length of longer side = (x + 14) m
Using pythagoras theorem,
(l)² + (b)² = (h)²
∴ x² + (x + 14)2² = (x + 16)²
⇒ x² + x² + 196 + 28x = x² + 256 + 32x
⇒ x² – 4x – 60 = 0
⇒ x² – 10x + 6x – 60 = 0
⇒ x(x – 10) + 6(x – 10) = 0
⇒ (x – 10) (x + 6) = 0
⇒ x – 10 = 0 or x + 6 = 0
⇒ x = 10 or x = -6 (Reject)
⇒ x = 10 m …[As length cannot be negative
Length of shorter side = x = 10 m
Length of diagonal = (x + 16) m = 26 m
Length of longer side = (x + 14)m = 24m
∴ Length of sides are 10 m and 24 m.

Question 65.
The sum of three numbers in A.P. is 12 and sum of their cubes is 288. Find the numbers. (2016D)
Solution:
Let three numbers in A.P. are a – d, a, a + d.
a – d + a + a + d = 12
⇒ 3a = 12 ⇒a = 4
(a – d)³ + (a)³ + (a + d)³ = 288
⇒ a³ – 3a²d + 3ad² – d³ + a³ + a³ + 3a²d + 3ad² + d³ = 288
⇒ 3a³ + 6ad² = 288
⇒ 3a(a² + 2d²) = 288
⇒ 3 × 4(4² + 2d²) = 288
⇒ (16 + 2d²) = 28812
⇒ 2d² = 24 – 16 = 8
⇒ d² = 4 ⇒ d = ± 2
When, a = 4, d = 2, numbers are –
a – d, a, a + d, i.e., 2, 4, 6
When, a = 4, d = -2, numbers are –
a – d, a, a + d, i.e., 6, 4, 2

Question 66.
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle. (2016D)
Solution:

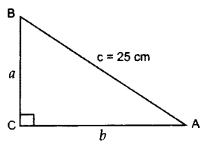
Perimeter of right ∆ = 60 cm …[Given
a + b + c = 60
a + b + 25 = 60
a + b = 60 – 25 = 35 …(i)
In rt. ∆ACB, AC² + BC² = AB²
b² + a² = (25)² …[Pythagoras’ theorem
a² + b² = 625 ….(ii)
From (i), a + b = 35
(a + b)² = (35) … [Squaring both sides
a² + b² + 2ab = 1225
625 + 2ab = 1225 … [From (ii)
2ab = 1225 – 625 = 600 ⇒ ab = 300 … (iii)
Area of ∆ = 12 × base × corresponding altitude
= 12 × b × a = 12 (300) ..[From (iii)
= 150 cm²

Question 67.
The sum of two numbers is 9 and the sum of their reciprocals is 12. Find the numbers. (2012D)
Solution:
Let the numbers be x and 9 – x.
According to the Question,
1x+19−x=12
9−x+xx(9−x)=12
⇒ 18 = 9x – x²
⇒ x² – 9x + 18 = 0
⇒ x² – 3x – 6x + 18 = 0
⇒ x(x – 3) – 6(x – 3) = 0
⇒ (x – 3) (x – 6) = 0
⇒ x – 3 = 0 or x – 6 = 0
⇒ x = 3 or x = 6
When x = 3, nos. are 3 and 6.
When x = 6, nos. are 6 and 3.

Question 68.
The numerator of a fraction is 3 less than its denominator. If 1 is added to the denominator, the fraction is decreased by 115. Find the fraction. (20120D)
Solution:
Let the denominator be x and the numerator be x – 3.
∴ Fraction =x−3x
New denominator = x + 1
According to the Question,

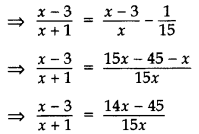
⇒ 15x² – 45x = 14x² – 45x + 14x – 45
⇒ 15x² – 14x² – 14x + 45 = 0
⇒ x² – 14x + 45 = 0
⇒ x² – 5x – 9x + 45 = 0
⇒ x(x – 5) – 9(x – 5) = 0
⇒ (x – 5) (x – 9) = 0
⇒ x – 5 = 0 or x – 9 = 0
⇒ x = 5 or x = 9
When x = 5, fraction = 5−35=25
When x = 9, fraction = 9−39=69=23
∴ Fraction = 25 or 23

Question 69.
The difference of two natural numbers is 5 and the difference of their reciprocals is 110. Find the numbers. (2014D)
Solution:
Let the larger natural number be x and the smaller natural number be y.
According to the Question,

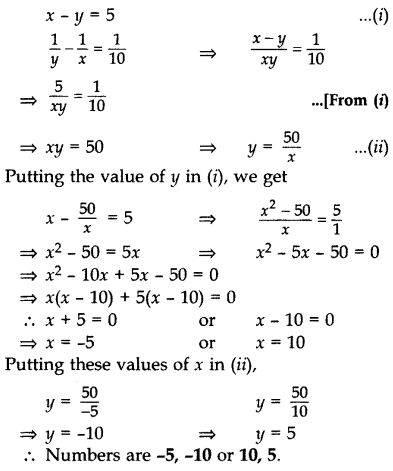
Question 70.
The difference of two natural numbers is 5 and the difference of their reciprocals is 514. Find the numbers. (2014D)
Solution:
Let the larger number be x and the smaller number be y.
According to the Question,

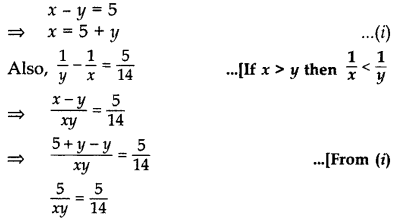
⇒ xy = 14
(5 + y)y = 14 … [From (i)
y² + 5y – 14 = 0
⇒ y² + 7y – 2y – 14 = 0
y(y + 7) – 2(y + 7) = 0
(y – 2) (y + 7) = 0
y – 2 = 0 or y + 7 = 0
y = 2 or y = -7
When y = 2, x = 5 + 2 = 7 …[From (1)
∴ Numbers are 7 and 2.
When y = -7, x = 5 + (-7) = -2 …[From (i)
∴ Numbers are -2 and (-7).

Question 71.
The numerator of a fraction is 3 less than its denominator. If 2 is added to both the numerator and the denominator, then the sum of the new fraction and original fraction is a 2920. Find the original fraction. (2015D)
Solution: .
Let the denominator and numerator of the
fraction be x and x – 3 respectively.
Let the fraction be x−3x.
By the given condition,

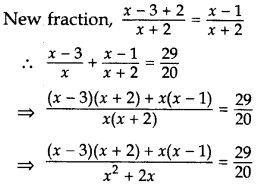
⇒ 20[(x – 3) (x + 2) + x(x – 1)] = 29(x² + 2x)
⇒ 20(x² – x – 6 + x² – x) = 29x² + 58x
⇒ 20(2x² – 2x – 6) = 29x² + 58x
⇒ 40x² – 29x² – 40x – 58x = 120
⇒ 11x² – 98x – 120 = 0
⇒ 11x² – 110x + 12x – 120 = 0
⇒ 11x(x – 10) + 12(x – 10) = 0
⇒ (11x + 12) (x – 10) = 0
⇒ 11x + 12 = 0 or x – 10 = 0
⇒ x = −1211 (Reject) or x = 10
Now denominator (x) = 10
then, numerator = x – 3 = 7
∴ The fraction is 1o.

Question 72.
A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m. Find the length and breadth of the rectangular park. (2016OD)
Solution:
Let length of the rectangular park = x m,
breadth of the rectangular park = (x -3)m
∴ Area of the rectangular park = x(x – 3)m²… (i)
Base of an isosceles triangle = (x – 3)m
Altitude of an isosceles triangle = 12 m
∴ Area of isosceles triangle
= 1/2 × base × altitude
= 1/2 × (x – 3) × 12
= 6(x – 3) …(ii)
According to the question,
Ar.(rectangle) – Ar.(isosceles ∆) = 4 m²
⇒ x(x – 3) – 6(x – 3) = 4 … [From (i) & (ii)
⇒ x² – 3x – 6x + 18 – 4 = 0
⇒ x² – 9x + 14 = 0
⇒ x² – 7x – 2x + 14 = 0
⇒ x(x – 7) – 2(x – 7) = 0
⇒ (x – 2) (x – 7) = 0
⇒ x – 2 = 0 or x – 7 = 0
⇒ x = 2 or x = 7
When x = 2, breadth of rectangle becomes -ve, so this is not possible.
∴ Length of the rectangular park, x = 7 m
and Breadth = (x – 3) = 4 m.

Question 73.
A train travels 180 km at a uniform speed. If the speed had been 9 km/hour more, it would have taken 1 hour less for the same journey. Find the speed of the train. (2011OD)
Solution:
Let the speed of the train = x km/hr
Let the increased speed of the train = (x + 9) km/hr
According to the question,

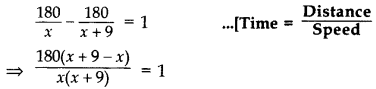
⇒ x(x + 9) = 1620
⇒ x² + 9x – 1620 = 0
⇒ x² + 45x – 36x – 1620 = 0
⇒ x(x + 45) – 36(x + 45) = 0
⇒ (x – 36) (x + 45) = 0
⇒ x – 36 = 0 or x + 45 = 0
⇒ x = 36 or x = -45 ….[Rejecting negative value as the speed cannot be -ve
∴ Speed of the train = 36 km/hr

Question 74.
In a flight of 2800 km, an aircraft was slowed down due to bad weather. Its average speed is reduced by 100 km/h and time increased by 30 minutes. Find the original duration of the flight. (2012OD)
Solution:
Let the average speed of the aircraft = x km/hr
the reduced speed of the aircraft = (x – 100 km/hr
Then Distance = 2800 km
According to the Question,

⇒ x² – 100x = 560000
⇒ x² – 100x – 560000 = 0
⇒ x² – 800x + 700x – 560000 = 0
⇒ x(x – 800) + 700(x – 800) = 0
⇒ (x – 800) (x + 700) = 0
⇒ x – 800 = 0 or x + 700 = 0
⇒ x = 800 or x = -700
As speed of the aircraft cannot be -ve.
∴ Speed = 800 km/hr
∴ Original duration/time = Distance  Speed 
= 2800800=72
= 31/2 hrs. or 3 hrs. 30 mins. or 210 mins.

Question 75.
While boarding an aeroplane, a passenger got hurt. The pilot, showing promptness and concern, made arrangements to hospitalise the injured and so the plane started late by 30 minutes. To reach the destination, 1500 km away in time, the pilot increased the speed by 100 km/hour. Find the original speed/hour of the plane. (2013OD)
Solution:
Let the original speed of the aeroplane = x km/hr
The increased speed of the aeroplane = (x + 100) km/hr
Given: Distance = 1500 km
According to the Question,

⇒ x(x + 100) = 300000
⇒ x² + 100x – 300000 = 0
⇒ x² + 600x – 500x – 300000 = 0
⇒ x(x + 600) – 500(x + 600) = 0
⇒ (x – 500) (x + 600) = 0
⇒ x – 500 = 0 or x + 600 = 0
⇒ x = 500 or x = -600 (rejected)
Since speed cannot be negative.
∴ Original speed of the aeroplane = 500 km/hr
Original time =  Distance  Speed =1,500500 = 3 hrs.

Question 76.
A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed? (2015OD)
Solution:
Let the original average speed of (first) train be x km/hr.
Now, new speed will be = (x + 6) km/hr.
We know,

⇒ 54x + 324 + 63x = 3x (x + 6)
⇒ 117x + 324 = 3x² + 18x
⇒ 3x² + 18x – 117x – 324 = 0
⇒ 3x² – 99x – 324 = 0
⇒ x² – 33x – 108 = 0
⇒ x² – 36x + 3x – 108 = 0
⇒ x(x – 36) + 3(x – 36) = 0
⇒ (x – 36) (x + 3) = 0
⇒ x – 36 = 0 or x + 3 = 0
x = 36 or x = -3 (Reject)
∴ First speed of train = 36 km/h.

Question 77.
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed. (2015OD)
Solution:
Let the first average speed of the bus be x km/hr.
Now, new speed of bus = (x + 10) km/hr.


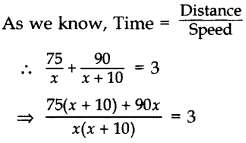
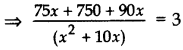
⇒ 75x + 750 + 90x = 3(x² + 10x)
⇒ 165x + 750 – 3x² – 30x = 0
⇒ 3x² – 135x – 750 = 0
⇒ x² – 45x – 250 = 0
⇒ x² – 50x + 5x – 250 = 0
⇒ x(x – 50) + 5(x – 50) = 0
⇒ (x – 50) (x + 5) = 0
∴ x = 50 or x = -5 (Reject)
∴ Speed = 50 km/h

Question 78.
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck. (2015OD)
Solution:
Let the first average speed of truck be x km/hr.

⇒ 150x + 3000 + 200x = 5(x² + 20x)
⇒ 350x + 3000 – 5x² – 100x = 0
⇒ x² – 50x – 600 = 0
⇒ x² – 60x + 10x – 600 = 0
⇒ x(x – 60) + 10(x – 60) = 0
⇒ (x – 60) (x + 10) = 0
⇒ x – 60 = 0 or x + 10 = 0
⇒ x = 60 or x = -10 (Reject)
∴ Speed = 60 km/hr.

Question 79.
Two pipes running together can fill a tank in 1119 minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately. (2016OD)
Solution:
Let the quicker pipe take to fill the cistern = x minutes
Then the slower pipe takes to fill the cistern = (x + 3) minutes
According to Question,

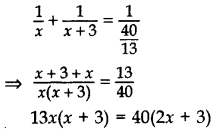
13xv + 39x = 80x + 120
13x² + 39x – 80x – 120 = 0
13x² – 41x – 120 = 0
13x² – 65x + 24x – 120 = 0
13x(x – 5) + 24(x – 5) = 0
(x – 5)(13x + 24) = 0
x – 5 = 0 or 13x + 24 = 0
x = 5 or x = −2413 (rejected) …[∵ x > 0
∴ x = 5 Hence, the faster pipe fills the cistern in 5 minutes, and the slower pipe fills the cistern in 8(5 + 3) minutes.

Question 80.
A motor boat whose speed is 20 km/h in still water, takes 1 hour more to go 48 km upstream than to return downstream to the same spot. Find the speed of the stream. (2011D)
Solution:
Let the speed of the stream be x km/hr
∴ Speed of the boat upstream = (20 – x) km/hr
and speed of the boat downstream = (20 + x) km/hr
Given, Distance = 48 km
According to the Question,

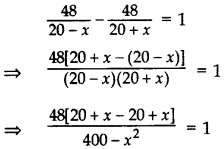
⇒ 96x = 400 – x²
⇒ x² + 96x – 400 = 0
⇒ x² + 100x – 4x – 400 = 0
⇒ x (x + 100) – 4 (x + 100) = 0
⇒ (x – 4) (x + 100) = 0
⇒ x – 4 = 0 or x + 100 = 0
⇒ x = 4 or x = – 100 ….[Rejecting negative value as the speed cannot be -ve
∴ Speed of the stream = 4 km/hr

Question 81.
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot.
Find the speed of the stream. (2014OD)
Solution:
Let speed of the stream be x km/hr,
Speed of the boat upstream = (18 – x) km/hr
and Speed of the boat downstream = (18 + x) km/hr
Given, Distance = 24 km
According to the Question,

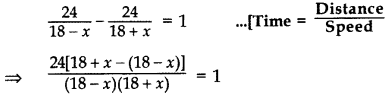
⇒ 24(2x)324−x2=1
⇒ 48x = 324 – x²
⇒ x² + 48x – 324 = 0
⇒ x² + 54x – 6x – 324 = 0
⇒ x(x + 54) – 6(x + 54) = 0
⇒ (x – 6) (x + 54) = 0
x – 6 = 0 or x + 54 = 0
x = 6 or x= -54 (rejected)
Since speed cannot be negative
∴ Speed of stream, x = 6 km/hr

Question 82.
The time taken by a person to cover 150 km was 2 hours more than the time taken in the return journey. If he returned at a speed of 10 km/hour more than the speed while going, find the speed per hour in each direction. (2016D)
Solution:
Let the speed of a person while going = x km/hr Then the speed of a person while returning = (x + 10) km/hr
Given, Distance = 150 km

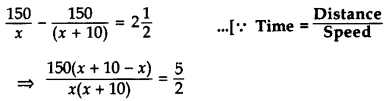
⇒ 5x(x + 10) = 3,000
⇒ x(x + 10) = 600 …[Dividing both sides by 5
⇒ x² + 10x – 600 = 0
⇒ x² + 30x – 20x – 600 = 0
⇒ x(x + 30) – 20(x + 30) = 0
⇒ (x + 30) (x – 20) = 0
⇒ x + 30 = 0 or x – 20 = 0
⇒ x = -30 (rejected) or x = 20
Since, speed can not be negative.
∴ Speed x = 20 km/hr.
∴ Speed while going = x = 20 km/hr
and Speed while returning
= (x + 10) = 20 + 10 = 30 km/hr

Question 83.
To fill a swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool. (2015D)
Solution:
Let the bigger pipe fill the tank in x hrs.
∴ the smaller pipe fills the tanks in (x + 10) hrs.

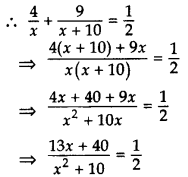
⇒ 2(13x + 40) = x² + 10x
⇒ 26x + 80 = x² + 10x
⇒ x² + 10x – 26x = 80
⇒ x² – 16x – 80 = 0
⇒ x² – 20x + 4x – 80 = 0
⇒ x(x – 20) + 4(x – 20) = 0
⇒ (x – 20) (x + 4) = 0
⇒ x – 20 = 0 or x + 4 = 0
x = 20 x = -4 (Reject)
Hence, the pipe with larger diameter fills the tank in 20 hours.
and the pipe with smaller diameter fills the tank in 30 hours.