Triangles Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
If ∆ABC ~ ∆PQR, perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC. (2012)
Solution:
∆ABC ~ ∆PQR …[Given

Question 2.
∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF. (2012, 2017D)
Solution:
∆ABC – ∆DEF …[Given

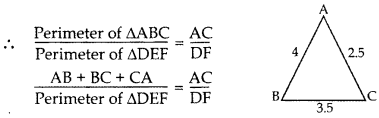
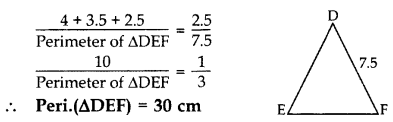
Question 3.
If ∆ABC ~ ∆RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10, then find QR. (2014)
Solution:
∆ABC ~ ∆RPQ …[Given

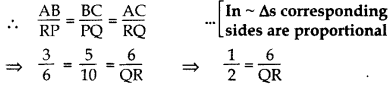
∴ QR = 12 cm

Question 4.
In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB. (2015)
Solution:
Let BD = x cm
then BW = (24 – x) cm, AE = 12 – 4 = 8 cm
In ∆DEW, AB || EW

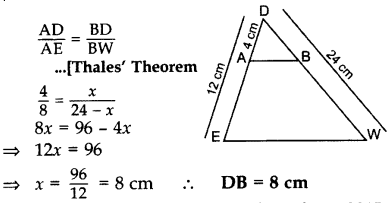
Question 5.
In ∆ABC, DE || BC, find the value of x. (2015)

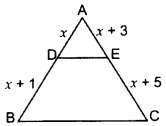
Solution:
In ∆ABC, DE || BC …[Given

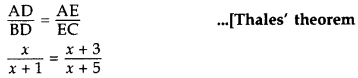
x(x + 5) = (x + 3)(x + 1)
x² + 5x = x² + 3x + x + 3
x² + 5x – x² – 3x – x = 3
∴ x = 3 cm

Question 6.
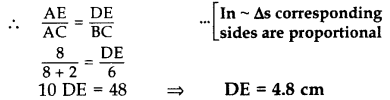
In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE. (2014)

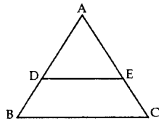
Solution:
In ∆ADE and ∆ABC,
∠DAE = ∠BAC …Common
∠ADE – ∠ABC … [Corresponding angles
∆ADE – ∆ΑΒC …[AA corollary

Question 7.
In the given figure, XY || QR, PQXQ=73 and PR = 6.3 cm, find YR. (2017OD)

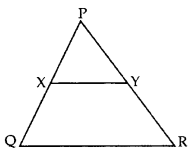
Solution:
Let YR = x
PQXQ=PRYR … [Thales’ theorem

Question 8.
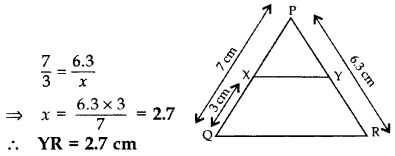
The lengths of the diagonals of a rhombus are 24 cm and 32 cm. Calculate the length of the altitude of the rhombus. (2013)
Solution:
Diagonals of a rhombus are ⊥ bisectors of each other.
∴ AC ⊥ BD,
OA = OC = AC2⇒242 = 12 cm
OB = OD = BD2⇒322 = 16 cm
In rt. ∆BOC,

Question 9.
If PQR is an equilateral triangle and PX ⊥ QR, find the value of PX². (2013)
Solution:
Altitude of an equilateral ∆,

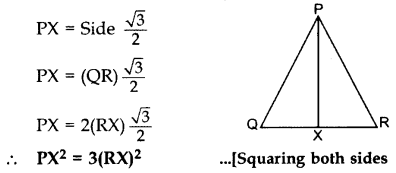
Triangles Class 10 Important Questions Short Answer-I (2 Marks)

Question 10.
The sides AB and AC and the perimeter P, of ∆ABC are respectively three times the corresponding sides DE and DF and the perimeter P, of ∆DEF. Are the two triangles similar? If yes, find ar(△ABC)ar(△DEF) (2012)
Solution:
Given: AB = 3DE and AC = 3DF

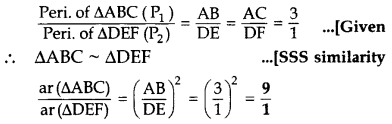
…[∵ The ratio of the areas of two similar ∆s is equal to the ratio of the squares of their corresponding sides

Question 11.
In the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF. (2014)

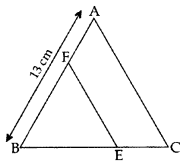
Solution:
BE = BC – EC = 10 – 2 = 8 cm
Let AF = x cm, then BF = (13 – x) cm
In ∆ABC, EF || AC … [Given

Question 12.
X and Y are points on the sides AB and AC respectively of a triangle ABC such that AXAB=14, AY = 2 cm and YC = 6 cm. Find whether XY || BC or not. (2015)
Solution:
Given: AXAB=14

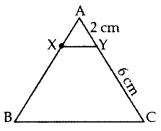
AX = 1K, AB = 4K
∴ BX = AB – AX
= 4K – 1K = 3K

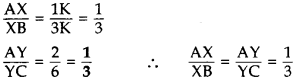
∴ XY || BC … [By converse of Thales’ theorem

Question 13.
In the given figure, ∠A = 90°, AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD. (2012; 2017D)

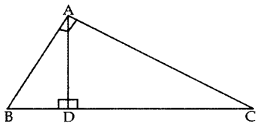
Solution:
∆ADB ~ ∆CDA …[If a perpendicular is drawn from the vertex of the right angle of a rt. ∆ to the hypotenuse then As on both sides of the ⊥ are similar to the whole D and to each other
∴ BDAD=ADCD …[∵ Sides are proportional
AD² = BD , DC
AD² = (2) (8) = 16 ⇒ AD = 4 cm

Question 14.
In ∆ABC, ∠BAC = 90° and AD ⊥ BC. Prove that AD\frac{B D}{A D}=\frac{A D}{C D} = BD × DC. (2013)
Solution:
In 1t. ∆BDA, ∠1 + ∠5 = 90°
In rt. ∆BAC, ∠1 + ∠4 = 90° …(ii)
∠1 + ∠5 = ∠1 + ∠4 …[From (i) & (ii)
.. ∠5 = ∠4 …(iii)
In ∆BDA and ∆ADC,

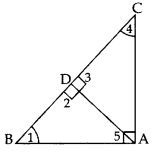
∠5 = 24 … [From (iii)
∠2 = ∠3 …[Each 90°
∴ ∆BDA ~ ∆ADC…[AA similarity
BDAD=ADCD
… [In ~ As corresponding BA sides are proportional
∴ AD² = BD × DC

Question 15.
A 6.5 m long ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall. Find the height of the wall where the top of the ladder touches it. (2015)
Solution:
Let AC be the ladder and AB be the wall.

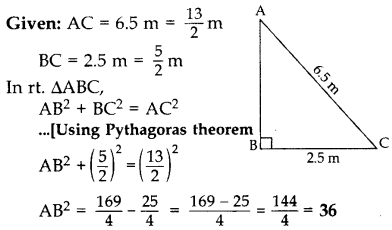
∴Required height, AB = 6 m

Question 16.
In the figure ABC and DBC are two right triangles. Prove that AP × PC = BP × PD. (2013)

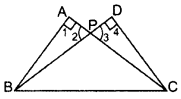
Solution:

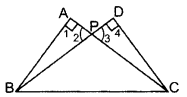
In ∆APB and ∆DPC,
∠1 = ∠4 … [Each = 90°
∠2 = ∠3 …[Vertically opp. ∠s
∴ ∆APB ~ ∆DPC …[AA corollary
⇒ BPPC=APPD … [Sides are proportional
∴ AP × PC = BP × PD

Question 17.
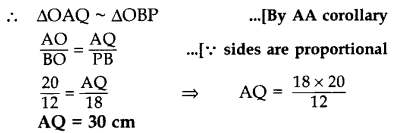
In the given figure, QA ⊥ AB and PB ⊥ AB. If AO = 20 cm, BO = 12 cm, PB = 18 cm, find AQuestion (2017OD)

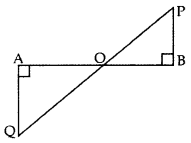
Solution:

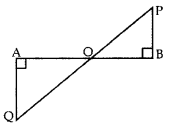
In ∆OAQ and ∆OBP,
∠OAQ = ∠OBP … [Each 90°
∠AOQ = ∠BOP … [vertically opposite angles

Triangles Class 10 Important Questions Short Answer-II (3 Marks)

Question 18.
In the given figure, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm. (2012)

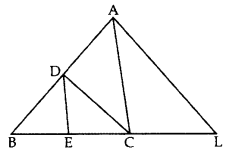
Solution:
In ∆ABL, CD || LA

Question 19.
If a line segment intersects sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, prove that ADAB=AEAC. (2013)
Solution:
Given. In ∆ABC, DE || BC

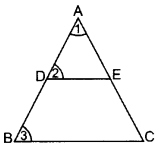
To prove. ADAB=AEAC
Proof.
In ∆ADE and ∆ABC
∠1 = ∠1 … Common
∠2 = ∠3 … [Corresponding angles
∆ADE ~ ∆ABC …[AA similarity
∴ ADAB=AEAC
…[In ~∆s corresponding sides are proportional

Question 20.
In a ∆ABC, DE || BC with D on AB and E on AC. If ADDB=34 , find BCDE. (2013)
Solution:
Given: In a ∆ABC, DE || BC with D on AB and E
on AC and ADDB=34
To find: BCDE
Proof. Let AD = 3k,

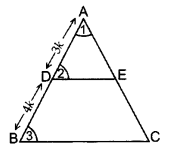
DB = 4k
∴ AB = 3k + 4k = 7k
In ∆ADE and ∆ABC,
∠1 = ∠1 …[Common
∠2 = ∠3 … [Corresponding angles
∴ ∆ADE ~ ∆ABC …[AA similarity

Question 21.
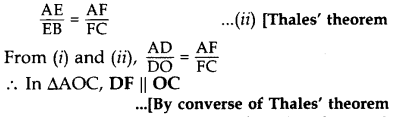
In the figure, if DE || OB and EF || BC, then prove that DF || OC. (2014)

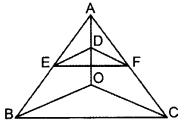
Solution:
Given. In ∆ABC, DE || OB and EF || BC
To prove. DF || OC
Proof. In ∆AOB, DE || OB … [Given

Question 22.
If the perimeters of two similar triangles ABC and DEF are 50 cm and 70 cm respectively and one side of ∆ABC = 20 cm, then find the corresponding side of ∆DEF. (2014)
Solution:

Given. ∆ABC ~ ∆DEF,
Perimeter(∆ABC) = 50 cm
Perimeter(∆DEF) = 70 cm
One side of ∆ABC = 20 cm
To Find. Corresponding side of ∆DEF (i.e.,) DE. ∆ABC ~ ∆DEF …[Given

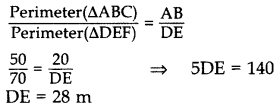
∴ The corresponding side of ADEF = 28 cm

Question 23.
A vertical pole of length 8 m casts a shadow 6 cm long on the ground and at the same time a tower casts a shadow 30 m long. Find the height of tower. (2014)
Solution:

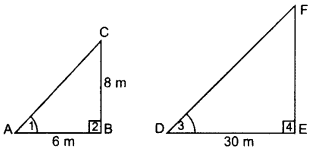
Let BC be the pole and EF be the tower Shadow AB = 6 m and DE = 30 m.
In ∆ABC and ∆DEF,
∠2 = ∠4 … [Each 90°
∠1 = ∠3 … [Sun’s angle of elevation at the same time
∆ABC ~ ∆DEF …[AA similarity
ABDE=BCEF … [In -As corresponding sides are proportional
⇒ 630=8EF ∴ EF = 40 m

Question 24.
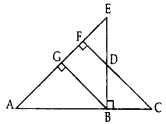
In given figure, EB ⊥ AC, BG ⊥ AE and CF ⊥ AE (2015)
Prove that:
(a) ∆ABG ~ ∆DCB
(b) BCBD=BEBA

Solution:

Given: EB ⊥ AC, BG ⊥ AE and CF ⊥ AE.
To prove: (a) ∆ABG – ∆DCB,
(b) BCBD=BEBA
Proof: (a) In ∆ABG and ∆DCB,
∠2 = ∠5 … [each 90°
∠6 = ∠4 … [corresponding angles
∴ ∆ABG ~ ∆DCB … [By AA similarity
(Hence Proved)
∴ ∠1 = ∠3 …(CPCT … [In ~∆s, corresponding angles are equal

(b) In ∆ABE and ∆DBC,
∠1 = ∠3 …(proved above
∠ABE = ∠5 … [each is 90°, EB ⊥ AC (Given)
∆ABE ~ ∆DBC … [By AA similarity
BCBD=BEBA
… [In ~∆s, corresponding sides are proportional
∴ BCBD=BEBA (Hence Proved)

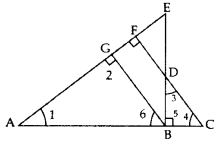
Question 25.
∆ABC ~ ∆PQR. AD is the median to BC and PM is the median to QR. Prove that ABPQ=ADPM. (2017D)
Solution:

∆ABC ~ ∆PQR … [Given
∠1 = ∠2 … [In ~∆s corresponding angles are equal

Question 26.
State whether the given pairs of triangles are similar or not. In case of similarity mention the criterion. (2015)

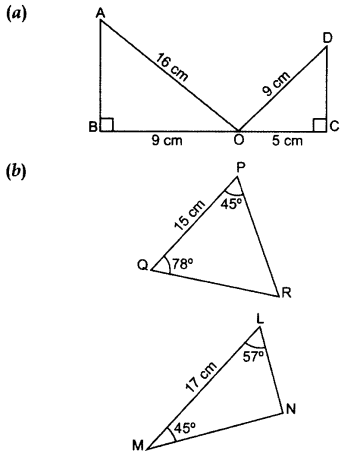
Solution:

(b) In ∆PQR, ∠P + ∠Q + ∠ZR = 180° …[Angle-Sum Property of a ∆
45° + 78° + ∠R = 180°
∠R = 180° – 45° – 78° = 57°
In ∆LMN, ∠L + ∠M + ∠N = 180° …[Angle-Sum Property of a ∆
57° + 45° + ∠N = 180°
∠N = 180° – 57 – 45° = 78°
∠P = ∠M … (each = 45°
∠Q = ∠N … (each = 78°
∠R = ∠L …(each = 57°
∴ ∆PQR – ∆MNL …[By AAA similarity theorem

Question 27.
In the figure of ∆ABC, D divides CA in the ratio 4 : 3. If DE || BC, then find ar (BCDE) : ar (∆ABC). (2015)

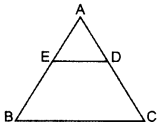
Solution:
Given:
D divides CA in 4 : 3
CD = 4K
DA = 3K
DE || BC …[Given

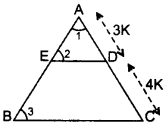
In ∆AED and ∆ABC,
∠1 = ∠1 …[common
∠2 = ∠3 … corresponding angles
∴ ∆AED – ∆ABC …(AA similarity
⇒ ar(△AED)ar(△ABC)=(ADAC)2
… [The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides
⇒ frac(3K)2(7K)2=9K249K2=ar(△AED)ar(△ABC)=949
Let ar(∆AED) = 9p
and ar(∆ABC) = 49p
ar(BCDE) = ar (∆ABC) – ar (∆ADE)
= 49p – 9p = 40p
∴ ar(BCDE)ar(△ABC)=40p49p
∴ ar (BCDE) : ar(AABC) = 40 : 49

Question 28.
In the given figure, DE || BC and AD : DB = 7 : 5, find \frac { ar\left( \triangle DEF \right) }{ ar\left( \triangle CFB \right) } [/latex] (2017OD)

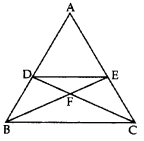
Solution:
Given: In ∆ABC, DE || BC and AD : DB = 7 : 5.
To find: ar(△DEF)ar(△CFB) = ?

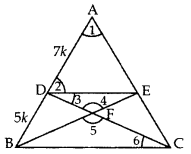
Proof: Let AD = 7k
and BD = 5k then
AB = 7k + 5k = 12k
In ∆ADE and ∆ABC,
∠1 = ∠1 …(Common
∠2 = ∠ABC … [Corresponding angles

Question 29.
In the given figure, the line segment XY is parallel to the side AC of ∆ABC and it divides the triangle into two parts of equal areas. Find the ratio AXAB. (2017OD)

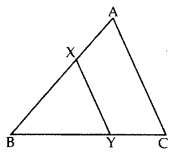
Solution:
We have XY || AC … [Given
So, ∠BXY = ∠A and ∠BYX = ∠C …[Corresponding angles
∴ ∆ABC ~ ∆XBY …[AA similarity criterion

Question 30.
In the given figure, AD ⊥ BC and BD = 13CD. Prove that 2AC² = 2AB² + BC². (2012)

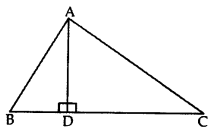
Solution:
BC = BD + DC = BD + 3BD = 4BD
∴ BC4 = BD
In rt. ∆ADB, AD² = AB² – BD² ….(ii)
In rt. ∆ADC, AD² = AC² – CD² …(iii)
From (ii) and (iii), we get
AC² – CD² = AB² – BD²
AC² = AB² – BD² + CD²

∴ 2AC² = 2AB² + BC² (Hence proved)

Question 31.
In the given figure, ∆ABC is right-angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE. (2012, 2017D)

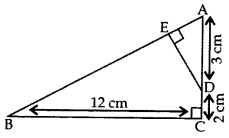
Solution:
Given: ∆ABC is rt. ∠ed at C and DE ⊥ AB.
AD = 3 cm, DC = 2 cm, BC = 12 cm
To prove:
(i) ∆ABC ~ ∆ADE; (ii) AE = ? and DE = ?
Proof. (i) In ∆ABC and ∆ADE,
∠ACB = ∠AED … [Each 90°
∠BAC = ∠DAE …(Common .
∴ ∆ABC ~ ∆ADE …[AA Similarity Criterion

(ii) ∴ ABAD=BCDE=ACAE … [side are proportional
AB3=12DE=3+2AE
…..[In rt. ∆ACB, … AB² = AC² + BC² (By Pythagoras’ theorem)
= (5)² + (12)² = 169
∴ AB = 13 cm

Question 32.
In ∆ABC, if AP ⊥ BC and AC² = BC² – AB², then prove that PA² = PB × CP. (2015)
Solution:

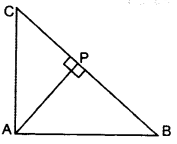
AC² = BC² – AB² …Given
AC² + AB² = BC²
∴ ∠BAC = 90° … [By converse of Pythagoras’ theorem
∆APB ~ ∆CPA
[If a perpendicular is drawn from the vertex of the right angle of a triangle to the hypotenuse then As on both sides of the perpendicular are similar to the whole triangle and to each other.
∴ APCP=PBPA … [In ~∆s, corresponding sides are proportional
∴ PA² = PB. CP (Hence Proved)

Question 33.
ABCD is a rhombus. Prove that AB² + BC² + CD² + DA² = AC² + BD². (2013)
Solution:
Given. In rhombus ABCD, diagonals AC and BD intersect at O.

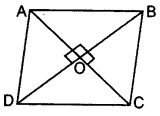
To prove: AB² + BC² + CD² + DA² = AC² + BD²
Proof: AC ⊥ BD [∵ Diagonals of a rhombus bisect each other at right angles
∴ OA = OC and
OB = OD
In rt. ∆AOB,
AB² = OA² + OB² … [Pythagoras’ theorem
AB² = (AC2)2+(BD2)2
AB² = (AC2)2+(BD2)2
4AB² = AC² + BD²
AB² + AB² + AB² + AB² = AC² + BD²
∴ AB² + BC² + CD² + DA² = AC² + BD²
…[∵ In a rhombus, all sides are equal

Question 34.
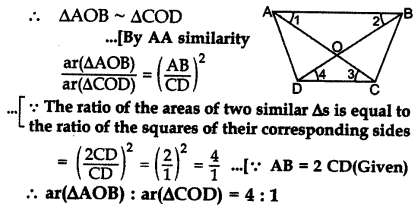
The diagonals of trapezium ABCD intersect each other at point o. If AB = 2CD, find the ratio of area of the ∆AOB to area of ∆COD. (2013)
Solution:
In ∆AOB and ∆COD, … [Alternate int. ∠s
∠1 = ∆3
∠2 = ∠4

Question 35.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium. (2014)
Solution:
1st method.
Given: Quadrilateral ABCD in which
AC and BD intersect each other at 0.
Such that AOBO=CODO
To prove: ABCD is a trapezium
Const.: From O, draw OE || CD.


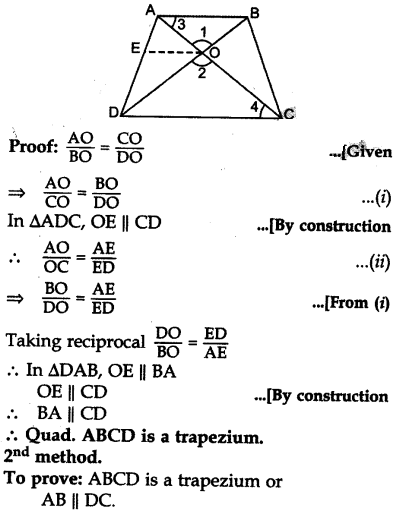
But these are alternate interior angles
∴ AB || DC Quad. ABCD is a trapezium.

Triangles Class 10 Important Questions Long Answer (4 Marks).

Question 36.
In a rectangle ABCD, E is middle point of AD. If AD = 40 m and AB = 48 m, then find EB. (2014D)
Solution:

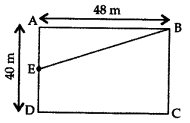
E is the mid-point of AD …[Given
AE = 402 = 20 m
∠A = 90° …[Angle of a rectangle
In rt. ∆BAE,
EB² = AB² + AE² …[Pythagoras’ theorem
= (48)² + (20)²
= 2304 + 400 = 2704
∴ EB = 2704−−−−√ = 52 m

Question 37.
Let ABC be a triangle and D and E be two points on side AB such that AD = BE. If DP || BC and EQ || AC, then prove that PQ || AB. (2013)
Solution:

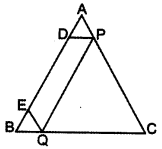
In ∆ABC,
DP || BC
and EQ || AC … [Given

Now, in ∆ABC, P and Q divide sides CA and CB respectively in the same ratio.
∴ PQ || AB

Question 38.
In the figure, ∠BED = ∠BDE & E divides BC in the ratio 2 : 1.
Prove that AF × BE = 2 AD × CF. (2015)

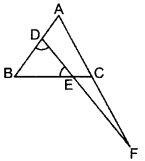
Solution:
Construction:
Draw CG || DF
Proof: E divides
BC in 2 : 1.
BEEC=21 …(i)

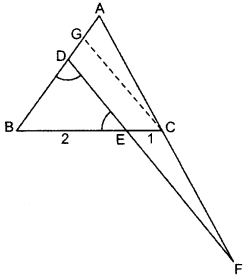
Question 39.
In the given figure, AD = 3 cm, AE = 5 cm, BD = 4 cm, CE = 4 cm, CF = 2 cm, BF = 2.5 cm, then find the pair of parallel lines and hence their lengths. (2015)

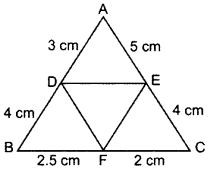
Solution:

Question 40.
If sides AB, BC and median AD of AABC are proportional to the corresponding sides PQ, QR and median PM of PQR, show that ∆ABC ~ ∆PQR. (2017OD)
Solution:

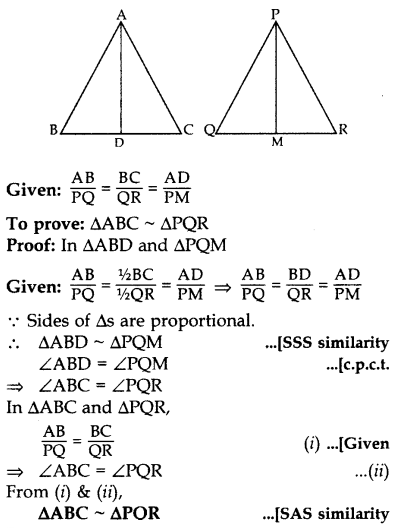
Question 41.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. (2012)
Solution:
Given: ∆ABC ~ ∆DEF

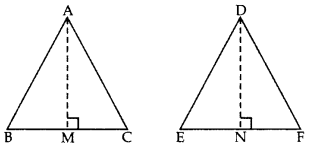
Question 42.
State and prove converse of Pythagoras theorem. Using the above theorem, solve the following: In ∆ABC, AB = 63–√ cm, BC = 6 cm and AC = 12 cm, find ∠B. (2015)
Solution:
Part I:
Statement: Prove that, in a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

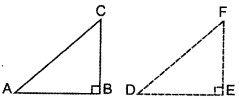
To prove: ∠ABC = 90°
Const.: Draw a right angle ∆DEF in which DE = BC and EF = AB.
Proof: In rt. ∆ABC,
AB² + BC² = AC² …(i) Given
In rt. ∆DEF
DE² + EF² = DF² … [By Pythagoras’ theorem
BC² + AB² = DF²…(ii)…[∵ DE = BC; EF = AB
From (i) and (ii), we get
AC² = DF² = AC = DF
Now, DE = BC …[By construction
EF = AB …[By construction
DF = AC … [Proved above :
∴ ∆DEF = ∆ABC … (SSS congruence :
∴ ∠DEF = ∠ABC …[c.p.c.t.
∵ ∠DEF = 90° ∴ ∠ABC = 90°
Given: In rt. ∆ABC,
AB² + BC² = AC²
AB² + BC² = (63–√)² + (6)²
= 108 + 36 = 144 = (12)²
AB² + BC² = AC² ∴ ∠B = 90° … [Above theorem

Question 43.
In the given figure, BL and CM are medians of a triangle ABC, right angled at A. Prove that: 4(BL² + CM²) = 5BC² (2012)

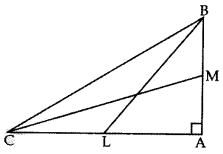
Solution:
Given: BL and CM are medians of ∆ABC, right angled at A.
To prove: 4(BL² + CM²) = 5 BC²
Proof: In ∆ABC, BC² = BA² + CA² …(i)
In ∆BAL,
BL² = BA² + AL² …[Pythagoras’ theorem
BL² = BA² + (CA2)2
BL² = BA²+ CA24
⇒ 4BL² = 4BA² + CA² …(ii)
Now, In ∆MCA,
MC² = CA² + MA² …[Pythagoras’ theorem
MC² = CA²2 + (BA2)2
MC² = CA² + BA24
4MC² = 4CA² + BA²
Adding (ii) and (iii), we get
4BL² + 4MC² = 4BA² + CA² + 4CA²+ BA² …[From (ii) & (iii)
4(BL² + MC²) = 5BA² + 5CA²
4(BL² + MC²) = 5(BA² + CA²)
∴ 4(BL² + MC²) = 5BC² … [Using (1)
Hence proved.

Question 44.
In the given figure, AD is median of ∆ABC and AE ⊥ BC. (2013)
Prove that b² + c² = 2p² + 12 a².

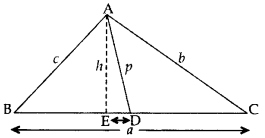
Solution:

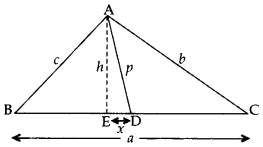
Proof. Let ED = x
BD = DC = BC2=a2 = …[∵ AD is the median
In rt. ∆AEC, AC² = AE² + EC² …..[By Pythagoras’ theorem
b² = h² + (ED + DC)²
b² = (p² – x²) + (x = a2)²
…[∵ In rt. ∆AED, x² + h² = p² ⇒ h² = p² – x² …(i)
b² = p² – x² + x² + (a2)2²+ 2(x)(a2)
b² = p² + ax + a24 …(ii)
In rt. ∆AEB, AB² = AE² + BE² … [By Pythagoras’ theorem

Question 45.
In a ∆ABC, the perpendicular from A on the side BC of a AABC intersects BC at D such that DB = 3 CD. Prove that 2 AB² = 2 AC² + BC². (2013; 2017OD)
Solution:
In rt. ∆ADB,
AD² = AB² – BD² …(i) [Pythagoras’ theorem
In rt. ∆ADC,
AD² = AC² – DC² …(ii) [Pythagoras’ theorem

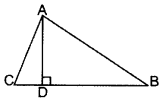
From (i) and (ii), we get
AB² – BD² = AC² – DC²
AB² = AC² + BD² – DC²
Now, BC = BD + DC
= 3CD + CD = 4 CD …[∵ BD = 3CD (Given)
⇒ BC² = 16 CD² …(iv) [Squaring
Now, AB² = AC² + BD² – DC² …[From (iii)
= AC² + 9 DC² – DC² ….[∵ BD = 3 CD ⇒ BD² = 9 CD²
= AC² + 8 DC²
= AC² + 16DC22
= AC² + BC22 … [From (iv)
∴ 2AB² = 2AC² + BC² … [Proved

Question 46.
In ∆ABC, altitudes AD and CE intersect each other at the point P. Prove that: (2014)
(i) ∆APE ~ ∆CPD
(ii) AP × PD = CP × PE
(iii) ∆ADB ~ ∆CEB
(iv) AB × CE = BC × AD
Solution:

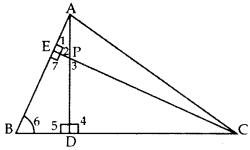
Given. In ∆ABC, AD ⊥ BC & CE ⊥ AB.
To prove. (i) ∆APE ~ ∆CPD
(ii) AP × PD = CP × PE
(iii) ∆ADB ~ ∆CEB
(iv) AB × CE = BC × AD
Proof: (i) In ∆APE and ∆CPD,
∠1 = ∠4 …[Each 90°
∠2 = ∠3 …[Vertically opposite angles
∴ ∆APE ~ ∆CPD …[AA similarity
(ii) APCP=PEPD … [In ~ ∆s corresponding sides are proportional
∴ AP × PD = CP × PE
(iii) In ∆ADB and ∆CEB,
∠5 = ∠7 …[Each 90°
∠6 = ∠6 …(Common
∴ ∆ADB ~ ∆CEB …[AA similarity
(iv) ∴ ABCB=ADCE … [In ~ ∆s corresponding sides are proportional
∴ AB × CE = BC × AD

Question 47.
In the figure, PQR and QST are two right triangles, right angled at R and T resepctively. Prove that QR × QS = QP × QT. (2014)

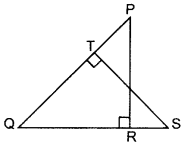
Solution:
Given: Two rt. ∆’s PQR and QST.

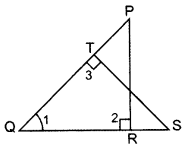
To prove: QR × QS = QP × QT
Proof: In ∆PRQ and ∆STQ,
∠1 = ∠1 … [Common
∠2 = ∠3 … [Each 90°
∆PRQ ~ ∆STO …(AA similarity
∴ QRQT=QPQS ..[In -∆s corresponding sides are proportional
∴ QR × QS = QP × QT (Hence proved)

Question 48.
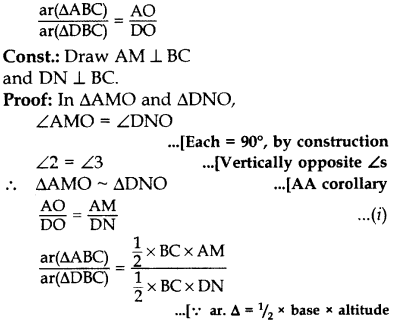
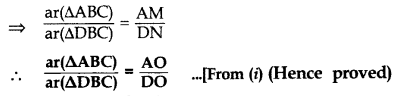
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO. (2012)

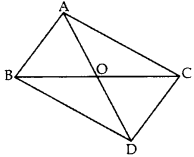
Solution:
Given: ABC and DBC are two As on the same base BC. AD intersects BC at O.
To prove:

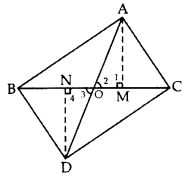
Question 49.
Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is longer than the other by 5 cm. Find the lengths of the other
two sides. (2013)
Solution:
Let Base, AB = x cm
Then altitude, BC = (x + 5) cm
In rt. ∆,
By Pythagoras’ theorem

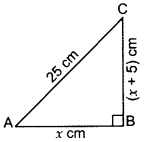
AB² + BC² = AC²
⇒ (x)² + (x + 5)² = 25²
⇒ x²2 + x² + 10x + 25 – 625 = 0
⇒ 2x² + 10x – 600 = 0
⇒ x² + 5x – 300 = 0 … [Dividing both sides by 2
⇒ x² + 20x – 15x – 300 = 0
⇒ x(x + 20) – 15(x + 20) = 0
(x – 15)(x + 20) = 0
x – 15 = 0 or x + 20 = 0
x = 15 or x = -20
Base cannot be -ve
∴ x = 15 cm
∴ Length of the other side = 15 + 5 = 20 cm
Two sides are = 15 cm and 20 cm

Question 50.
In Figure, AB ⊥ BC, FG ⊥ BC and DE ⊥ AC. Prove that ∆ADE ~ ∆GCF. (2016 OD)

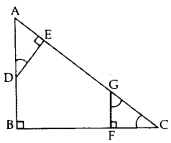
Solution:
In rt. ∆ABC,
∠A + ∠C = 90° …(i)
In rt. ∆AED,
∠A + ∠2 = 90°
From (i) and (ii), ∠C = ∠2
Similarly, ∠A = ∠1
Now in ∆ADE & ∆GCF
∠A = 1 … [Proved
∠C = 2 … [Proved
∠AED = ∠GFC … [rt. ∠s
∴ ∆ADE – ∆GCF …(Hence Proved)