Introduction to Trigonometry Class 10 Notes Maths Chapter 8

CBSE Class 10 Maths Notes Chapter 8 Introduction to Trigonometry Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 8 Introduction to Trigonometry. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

CBSE Class 10 Maths Notes Chapter 8 Introduction to Trigonometry

  • Position of a point P in the Cartesian plane with respect to co-ordinate axes is represented by the ordered pair (x, y).
  • Trigonometry is the science of relationships between the sides and angles of a right-angled triangle.
  • Trigonometric Ratios: Ratios of sides of right triangle are called trigonometric ratios.
    Consider triangle ABC right-angled at B. These ratios are always defined with respect to acute angle ‘A’ or angle ‘C.
  • If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios of an angle can be easily determined.
  • How to identify sides: Identify the angle with respect to which the t-ratios have to be calculated. Sides are always labelled with respect to the ‘θ’ being considered.

Let us look at both cases:
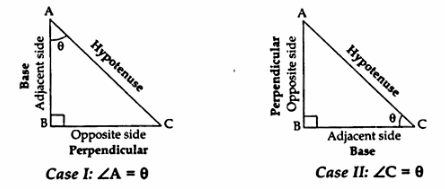
Introduction to Trigonometry Class 10 Notes Maths Chapter 8 Q1.1
In a right triangle ABC, right-angled at B. Once we have identified the sides, we can define six t-Ratios with respect to the sides.

case I case II
(i) sine A = perpendicularhypotenuse=BCAC (i) sine C = perpendicularhypotenuse=ABAC
(ii) cosine A = basehypotenuse=ABAC (ii) cosine C = basehypotenuse=BCAC
(iii) tangent A = perpendicularbase=BCAB (iii) tangent C = perpendicularbase=ABBC
(iv) cosecant A = hypotenuseperpendicular=ACBC (iv) cosecant C = hypotenuseperpendicular=ACAB
(v) secant A = hypotenusebase=ACAB (v) secant C = hypotenusebase=ACBC
(v) cotangent A = baseperpendicular=ABBC (v) cotangent C = baseperpendicular=BCAB

Note from above six relationships:

cosecant A = 1sinA, secant A = 1cosineA, cotangent A = 1tanA,

However, it is very tedious to write full forms of t-ratios, therefore the abbreviated notations are:
sine A is sin A
cosine A is cos A
tangent A is tan A
cosecant A is cosec A
secant A is sec A
cotangent A is cot A

TRIGONOMETRIC IDENTITIES

An equation involving trigonometric ratio of angle(s) is called a trigonometric identity, if it is true for all values of the angles involved. These are:
tan θ = sinθcosθ
cot θ = cosθsinθ

  • sin² θ + cos² θ = 1 ⇒ sin² θ = 1 – cos² θ ⇒ cos² θ = 1 – sin² θ
  • cosec² θ – cot² θ = 1 ⇒ cosec² θ = 1 + cot² θ ⇒ cot² θ = cosec² θ – 1
  • sec² θ – tan² θ = 1 ⇒ sec² θ = 1 + tan² θ ⇒ tan² θ = sec² θ – 1
  • sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1

ALERT:
A t-ratio only depends upon the angle ‘θ’ and stays the same for same angle of different sized right triangles.
Introduction to Trigonometry Class 10 Notes Maths Chapter 8 Q1.2
Value of t-ratios of specified angles:

∠A 0° 30° 45° 60° 90°
sin A 0 12 12√ 3√2 1
cos A 1 3√2 12√ 12 0
tan A 0 13√ 1 √3 not defined
cosec A not defined 2 √2 23√ 1
sec A 1 23√ √2 2 not defined
cot A not defined √3 1 13√ 0

The value of sin θ and cos θ can never exceed 1 (one) as opposite side is 1. Adjacent side can never be greater than hypotenuse since hypotenuse is the longest side in a right-angled ∆.

‘t-RATIOS’ OF COMPLEMENTARY ANGLES
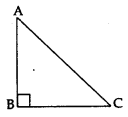
Introduction to Trigonometry Class 10 Notes Maths Chapter 8 Q1.3
If ∆ABC is a right-angled triangle, right-angled at B, then
∠A + ∠C = 90° [∵ ∠A + ∠B + ∠C = 180° angle-sum-property]
or ∠C = (90° – ∠A)

Thus, ∠A and ∠C are known as complementary angles and are related by the following relationships:
sin (90° -A) = cos A; cosec (90° – A) = sec A
cos (90° – A) = sin A; sec (90° – A) = cosec A
tan (90° – A) = cot A; cot (90° – A) = tan A