NCERT Solutions For Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
NCERT Solutions For Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Get Free NCERT Solutions for Class 10 Maths Chapter 7 Ex 7.1 Coordinate Geometry Class 10 Maths NCERT Solutions are extremely helpful while doing homework. Exercise 7.1 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 7 Maths Class 10 Coordinate Geometry Exercise 7.1 Provided in NCERT Textbook
Topics and Sub Topics in Class 10 Maths Chapter 7 Coordinate Geometry:
| Section Name | Topic Name |
| 7 | Coordinate Geometry |
| 7.1 | Introduction |
| 7.2 | Distance Formula |
| 7.3 | Section Formula |
| 7.4 | Area of a Triangle |
| 7.5 | Summary |
NCERT Solutions For Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 7 |
| Chapter Name | Coordinate Geometry |
| Exercise | Ex 7.1 |
| Number of Questions Solved | 10 |
| Category | NCERT Solutions |
Ex 7.1 Class 10 Maths Question 1.
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b)
Solution:
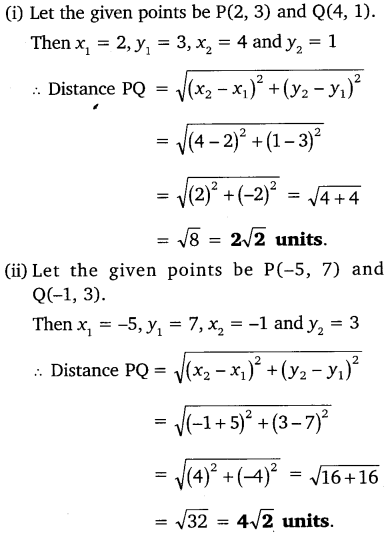
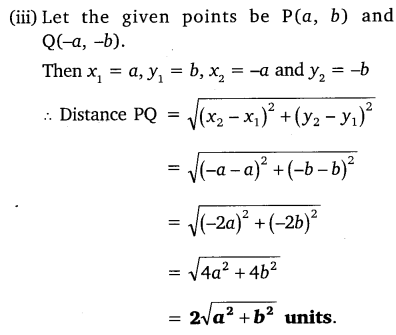
Ex 7.1 Class 10 Maths Question 2.
Find the distance between the points (0, 0) and (36, 15).
Solution:
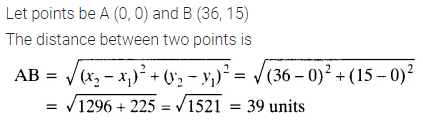
You can also download the free PDF of Chapter 7 Ex 7.1 Coordinate Geometry NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Download NCERT Solutions For Class 10 Maths Chapter 7 Coordinate Geometry PDF
Ex 7.1 Class 10 Maths Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
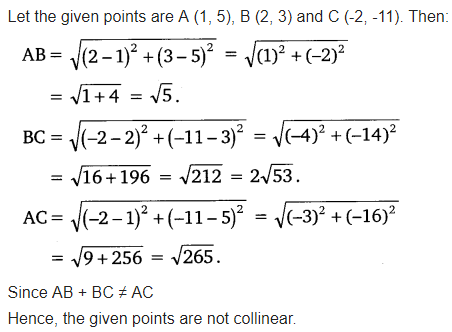
Ex 7.1 Class 10 Maths Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
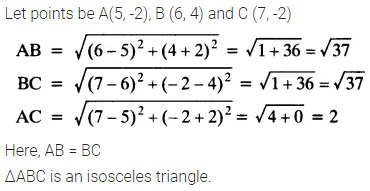
Ex 7.1 Class 10 Maths Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the given figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
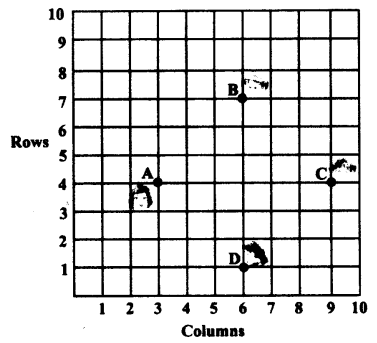
Solution:

Ex 7.1 Class 10 Maths Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:


Ex 7.1 Class 10 Maths Question 7.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
Solution:

Ex 7.1 Class 10 Maths Question 8.
Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.
Solution:
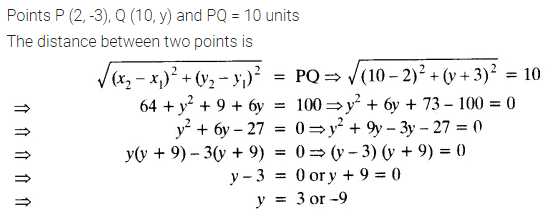
Ex 7.1 Class 10 Maths Question 9.
If Q (0, 1) is equidistant from P (5, -3), and R (x, 6), find the values of x. Also, find the distances QR and PR.
Solution:
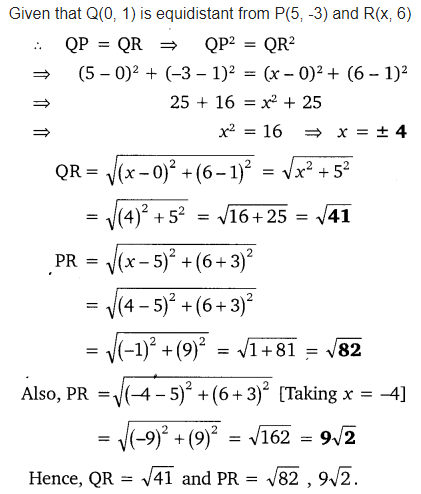
Ex 7.1 Class 10 Maths Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).
Solution:
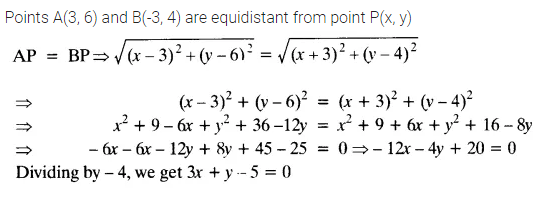
Class 10 Maths Coordinate Geometry Mind Maths
Coordinate of a Point in XY – Plane
The Perpendicular distance of x a point from the y-axis is called its x-coordinate or abscissa. The perpendicular distance y of a point from the x-axis is called its y-coordinate or ordinate. The x and y taken together in order is called coordinte of point denoted by (x, y).
The coordinate of the points on x-axis are of the form (x, 0) and the points on the y-axis are of the form(0, y). Coordinate of origin is (0, 0).
Sign-conventions in the XY-Plane
The x and y-axis divide the plane into four parts known as quadrants denoted by I, II, III and IV. The sign of x and y-coordinates in each of the quadrant is shown below:
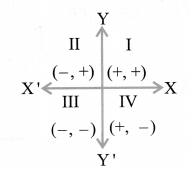
Distance Formula
The distance between any two points
P(x1, y1) and Q(x2, y2) in the plane is given by,
![]()
Also the distance of the point P(x1, y1) from the origin is
![]()
Section Formula
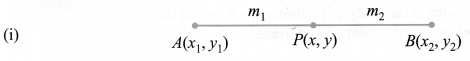
The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) internally in the ratio m1 : m2 i.e., PAPB=m1m2
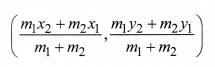
The coordinates of the point P(x, y) which divides the line segment joining the points A(x1, y1) and B(x2, y2) externally in the ratio, m1 : m2 i.e., PAPB=m1m2 are
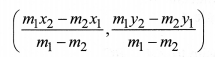
(iii) If the ratio in which P divides AB is K : 1, then the coordinates of the point P will be
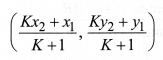
Mid-Point Formula
The coordinates of the mid point P of the line segment joining the points A(x1, y1) and B(x2, y2) is
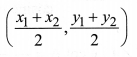
Area of a Triangle
The area of ∆ABC formed by the vertices A(x1, y1), B(x2, y2) is given by
![]()
Note:
(i) Area of triangle = 12 × base × Altitude
(ii) Area of polygon can be calculated by dividing it into the triangular region.
(iii) If three points are collinear then area of the triangle formed by them is zero.
