Topics and Sub Topics in Class 6 Maths Chapter 6 Integers

Section Name	Topic Name
7.1	Introduction
7.2	A Fraction
7.3	Fraction on the Number Line
7.4	Proper Fractions
7.5	Improper and Mixed Fractions
7.6	Equivalent Fractions
7.7	Simplest Form of a Fraction
7.8	Like Fractions
7.9	Comparing Fractions
7.9.1	Comparing Like Fractions
7.9.2	Comparing Unlike Fractions
7.10	Addition and Subtraction of Fractions
7.10.1	Adding or Subtracting like fractions
7.10.2	Adding or Subtracting fractions
7.10.3	How do we add or Subtract mixed fractions

Fractions Class 6 Ex 7.1

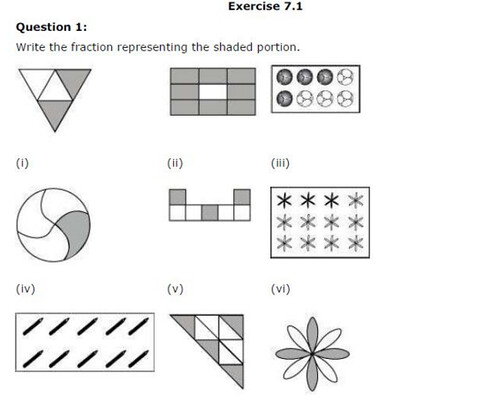
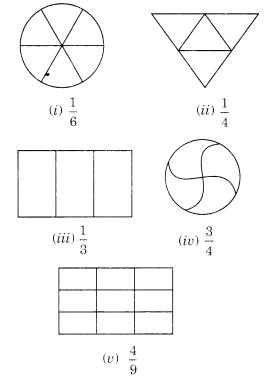
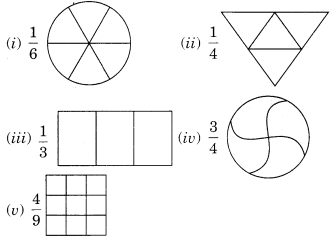
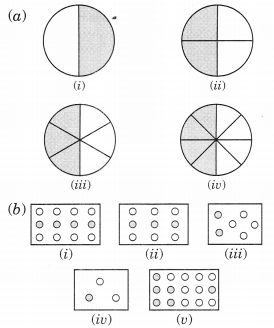
Ex 7.1 Class 6 Maths Question 1.
Write the fraction representing the shaded portion.

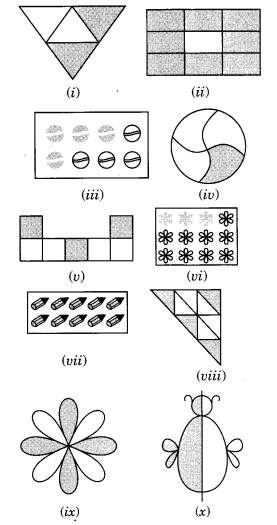
Solution:
(i) Total number of parts = 4
Number of shaded parts = 2
∴ Fraction = 24

(ii) Total number of parts = 9
Number of shaded parts = 8
∴ Fraction = 89

(iii) Total number of parts = 8
Number of shaded parts = 4
∴ Fraction = 48

(iv) Total number of parts = 4
Number of shaded parts = 1
∴ Fraction = 14

(v) Total number of parts = 7
Number of shaded parts = 3
∴ Fraction = 37

(vi) Total number of parts = 12
Number of shaded parts = 3
∴ Fraction = 312

(vii) Total number of parts = 10
Number of shaded parts = 10
∴ Fraction = 1010

(viii) Total number of parts = 9
Number of shaded parts = 4
∴ Fraction = 49

(ix) Total number of parts = 8
Number of shaded parts = 4
∴ Fraction = 48

(x) Total number of parts = 2
Number of shaded part = 1
∴ Fraction = 12

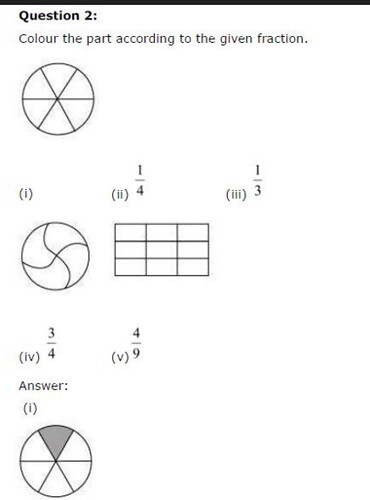
Ex 7.1 Class 6 Maths Question 2.
Colour the part according to the given fraction.

Solution:

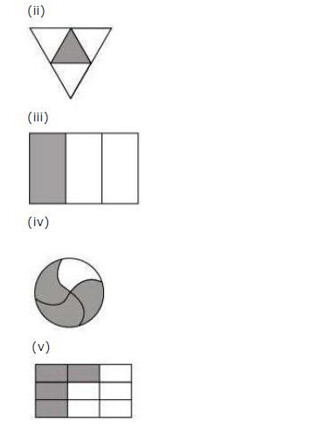
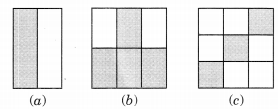
Ex 7.1 Class 6 Maths Question 3.
Identify the error, if any.

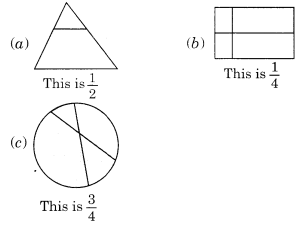
Solution:
(a) Since the shaded part is not half.
∴ This is not 12.

(b) Since, the parts are not equal.
∴ Shaded part is not 14 .

(c) Since, the part are not equal.
∴ Shaded part is not 34.

Ex 7.1 Class 6 Maths Question 4.
What fraction of a day is 8 hours?
Solution:
Since, a day has 24 hours and we have 8 hours,
∴ Required fraction = 824

Ex 7.1 Class 6 Maths Question 5.
What fraction of a hour is 40 minutes?
Solution:
Since I hours = 60 minutes
∴ Fraction of 40 minutes = 4060

Ex 7.1 Class 6 Maths Question 6.
Arya, Abhimanyu and Vivek shared lunch. Arya has brought two sandwiches, one made of vegetable and one of Jam. The other two boys forgot to bring their lunch. Arya agreed to share his sandwiches so that each person will have an equal share of each sandwich.
(a) How can Arya divide his sandwiches so that each person has an equal share?
(b) What part of a sandwich will each boy receive?
Solution:
(a) Arya has divided his sandwich into three equal parts.
So, each of them will get one part.
(b) Each one of them will receive 13 part.
∴ Required fraction = 13

Ex 7.1 Class 6 Maths Question 7.
Kanchan dyes dresses. She had to dye 30 dresses. She has so far finished 20 dresses. What fraction of dresses has she finished?
Solution:
Total number of dresses to be dyed = 30
Number of dresses finished = 20
∴ Required fraction = 2030 = 23

Ex 7.1 Class 6 Maths Question 8.
Write the natural numbers from 2 to 12. What fraction of them are prime numbers?
Solution:
Natural numbers between 2 and 12 are;
2,3,4, 5, 6, 7, 8, 9, 10,11, 12
Number of given natural numbers = 11
Number of prime numbers = 5
∴ Required fraction = 511

Ex 7.1 Class 6 Maths Question 9.
Write the natural numbers from 102 to 113. What fraction of them are prime numbers?
Solution:
Natural numbers from 102 to 113 are;
102,103,104,105,106, 107,108, 109,110, 111, 112,113
Total number of given natural numbers = 12
Prime numbers are 103, 107, 109, 113
∴ Number of prime numbers = 4
∴ Required fraction = 412 = 13

Ex 7.1 Class 6 Maths Question 10.
What fraction of these circles have X’s in them?

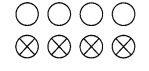
Solution:
Total number’of circles = 8
Number of circles having X’s in them = 4
Required fraction = 48 = 12

Ex 7.1 Class 6 Maths Question 11.
Kristin received a CD player for her birthday. She bought 3 CDs and received 5 others as gifts. What fraction of her total CDs did she buy and what fraction did she receive as gifts?
Solution:
Number of CDs bought by her from the market = 3
Number of CD’s received as gifts = 5
∴ Total number of CDs = 3 + 5 = 8
∴ Fraction of CD (bought) = 38 and the fraction of CDs (gifted) = 58

Fractions Class 6 Ex 7.2

Ex 7.2 Class 6 Maths Question 1.
Draw number lines and locate the points on them.

Solution:

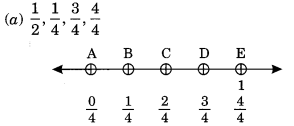
We have divided the number line from 0 to 1 into four equal parts.
C represents 24 i,e., 12
B represents 14
D represents 34
and E represents 44 , i.e., 1.

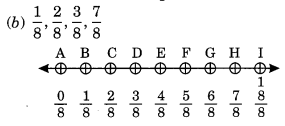
We have divided the number line from 0 to 1 into eight equal parts.
B represents 18
C represents 28
D represents 38
and H represents 78

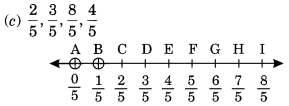
From the above number line, we have
C represents 25
D represents 35
E represents 45
and I represents 85

Ex 7.2 Class 6 Maths Question 2.
Express the following as mixed fractions:

Solution:

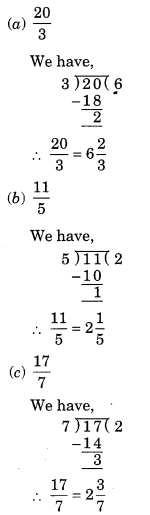
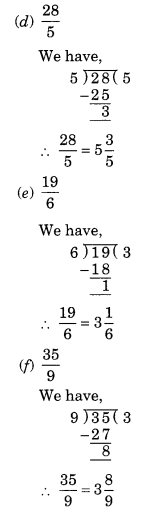
Ex 7.2 Class 6 Maths Question 3.
Express the following as improper fractions:

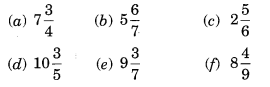
Solution:

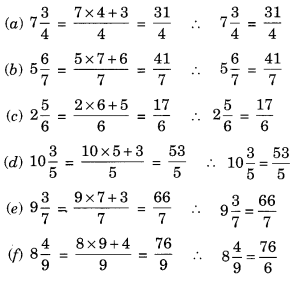
Fractions Class 6 Ex 7.3

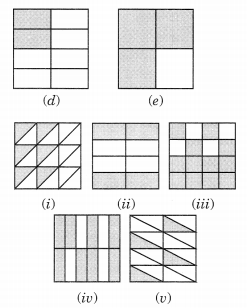
Ex 7.3 Class 6 Maths Question 1.
Write the fractions. Are all these fractions equivalent?

Solution:

Since all the fractions in their simplest form are not equal.
∴ They are not equivalent fractions.

Ex 7.3 Class 6 Maths Question 2.
Write the fractions and pair up the equivalent fractions from each row.


Solution:

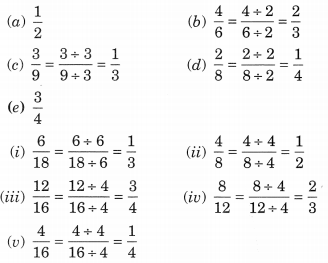
The following pairs fractions:represent the equivalent fractions.
(a) and (ii) = 12
(b) and (iv) = 23
(c) and (i) = 13
(d) and (v) = 14
(e) and (iii) = 34

Ex 7.3 Class 6 Maths Question 3.
Replace  in each of the following by the correct number:

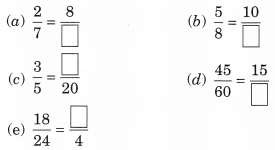
Solution:

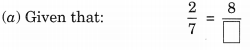
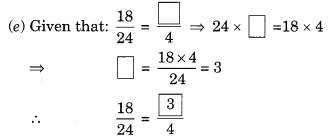
Ex 7.3 Class 6 Maths Question 4.
Find the equivalent fraction of 35 having
(a) denominator 20
(b) numerator 9
(c) denominator 30
(d) numerator 27
Solution:
(a) Here, we require denominator 20.
Let N be the numerator of the fractions.

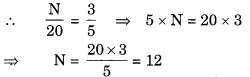
∴ The required fraction is 1220

(b) Here, we required numerator 9.
Let D be the denominator of the fraction.

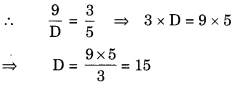
∴ The required fraction is 915.

(c) Here, we required denominator 30.
Let N be the numerator of the fraction.

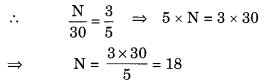
∴ The required fraction is 1830.

(d) Here, we required numerator 27.
Let D be the denominator of the fraction.

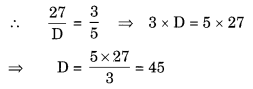
∴ The required fraction is 2745.

Ex 7.3 Class 6 Maths Question 5.
Find the equivalent fraction of 3648 with
(a) numerator 9
(b) denominator 4
Solution:
(a) Given that numerator = 9

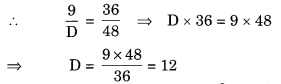
So, the equivalent fraction is 912.

(b) Given that denominator = 4
∴ N4 = 3648 ⇒ N x 48 = 4 x 36
⇒ N = 4x3648 = 3
So, the equivalent fraction is 34 .

Ex 7.3 Class 6 Maths Question 6.
Check whether the given fractions are equivalent:

Solution:
(a) 59 and 3054
We have 5 x 54 = 270
and 9 x 30 = 270
Here 5 x 54 = 9 x 30
∴ 59 and 3054 are equivalent fractions.

(b) 310 and 1250
We have 3 x 50 = 150
and 10 x 12 = 120
Here 3 x 50 ≠ 10 x 12
∴ 310 and 1250 are not equivalent fractions.

(c) 713 and 511
We have 7 x 11 = 77 and 5 x 13 = 65
Here 7 x 11 ≠ 5 x 13
∴ 713 and 511 are not equivalent fractions.

Ex 7.3 Class 6 Maths Question 7.
Reduce the following fractions to simplest form:

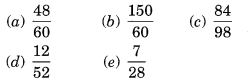
Solution:

Ex 7.3 Class 6 Maths Question 8.
Ramesh had 28 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up 10 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each use up? Check if each has used up an equal fraction of her/his pencils.
Solution:
Ramesh used up 10 pencils out of 20 pencils.

Sheelu used up 25 pencils out of 50 pencils.

Jamaal used up 40 pencils out of 80 pencils.

Yes, each has used up an equal fractions, i.e., 12.

Ex 7.3 Class 6 Maths Question 9.
Match the equivalent fractions and write two more for each.

Solution:


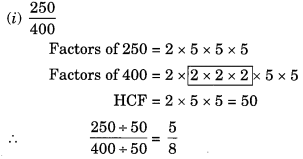
Two additional examples of equivalent fractions are

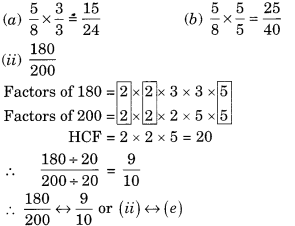
Two additional examples of equivalent fractions are

Two additional examples of equivalent fractions are

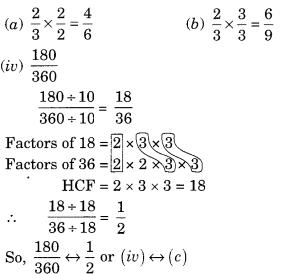
Two additional examples of equivalent fractions are


Two additional examples of equivalent fractions are

Fractions Class 6 Ex 7.4

Ex 7.4 Class 6 Maths Question 1.
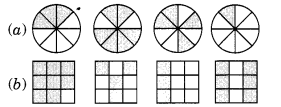
Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign ‘<‘, ‘=’, ‘>’ between the fractions.

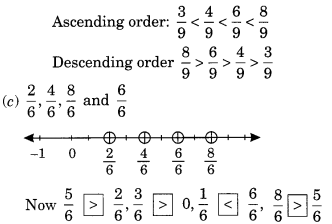
(c) Show 24 , 46 , 86 and 66 on the number line. Put appropriate signs between the fractions given.

Solution:
(a) Total number of divisions = 8
(i) Number of shaded parts = 3
∴ Fraction = 38

(ii) Total number of divisions = 8
Number of shaded parts = 6
∴ Fraction = 68

(iii) Total number of divisions = 8
Number of shaded parts = 4
∴ Fraction = 48

(iv) Total number of divisions = 8
Number of shaded part = 1
∴ Fraction = 18
Now the fractions are:
38, 68, 48 and 18 with same denominator.

(b)(i) Total number of divisions = 9
Number of shaded parts = 8
∴ Fraction = 89
(ii) Total number of divisions = 9
Number of shaded parts = 4
∴ Fraction = 49
(iii) Total number of divisions = 9
Number of shaded parts = 3
∴ Fraction = 39
(iv) Total number of divisions = 9
Number of shaded parts = 6
∴ Fraction = 69
∴ Fractions are 89, 49, 39, 69 with same denominator.

Ex 7.4 Class 6 Maths Question 2.
Compare the fractions and put an appropriate sign.

Solution:

Here, denominators of the two fractions are same and 3 < 5.

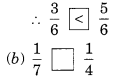
Here, numerators of the fractions are same and 7 > 4.

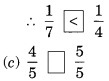
Here, denominators of the two fractions are same and 4 < 5.

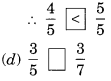
Here, numerators of the two fractions are same and 5 < 7.

Ex 7.4 Class 6 Maths Question 3.
Make five more such pairs and put appropriate signs.
Solution:

Ex 7.4 Class 6 Maths Question 4.
Look at the figures and write ’<’, or ’>’ ’=’ between the given pairs of fractions.

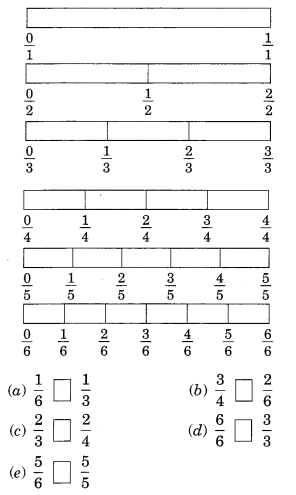
Make five more such problems and solve them with your friends
Solution:

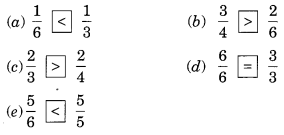
Make five more such problems yourself and solve them with your friends.

Ex 7.4 Class 6 Maths Question 5.
How quickly can you do this? Fill appropriate sign. ‘<‘, ‘=’, ‘>’.


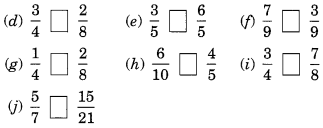
Solution:



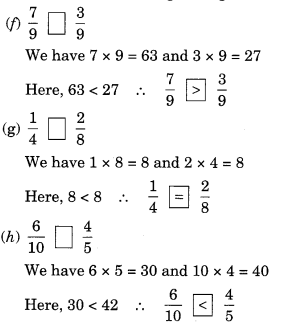
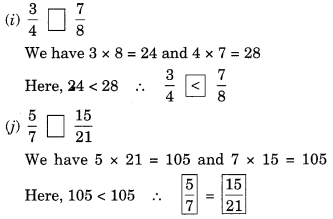
Ex 7.4 Class 6 Maths Question 6.
The following fractions represent just three different numbers. Separate them into three groups of equivalent fractions, by changing each one to its simplest form.

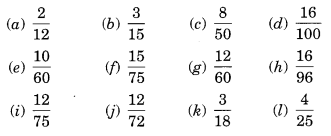
Solution:

Now grouping the above fractions into equivalent fractions, we have

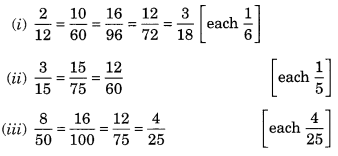
Ex 7.4 Class 6 Maths Question 7.
Find answers to the following. Write and indicate how you solved them.

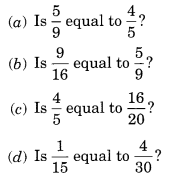
Solution:

By cross-multiplying, we get
5 x 5 = 25 and 4 x 9 = 36
Since 25 ≠ 36

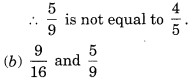
By cross-multiplying, we get
9 x 9 = 81 and 16 x 5 =80
Since 81 ≠ 80

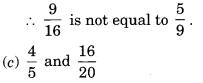
By cross-multiplying, we get
4 x 20 = 80 and 5 x 16 = 80
Since 80 = 80

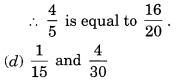
By cross-multiplying, we get
1 x 30 = 30 and 4 x 15 = 60

Ex 7.4 Class 6 Maths Question 8.
Ila read 25 pages of a book containing 100 pages.
Lalita read 25 of the same book. Who read less?
Solution:
Ila reads 25 pages out of 100 pages.

Lalita reads 25 of the same book.
Comparing 14 and 25 , we get
1 x 5 = 5 and 2 x 4 = 8
Since 5 < 8
∴ 14 < 25
Hence Ila reads less pages.

Ex 7.4 Class 6 Maths Question 9.
Rafiq exercised for 36 of an hour, while Rohit exercised for 34 of an hour. Who exercised for a longer time?
Solution:
Rafiq exercised for 36 of an hour.
Rohit exercised for 34 of an hour.
Comparing 36 and 34 , we get
3 x 4 = 12 and 3 x 6 = 18
Since 12 < 18
∴ 34 > 36
Hence Rohit exercised for longer time.

Ex 7.4 Class 6 Maths Question 10.
In a class A of 25 students, 20 passed in first class, in another class B of 30 students, 24 passed in first class. In which class was a greater fraction of students getting first class?
Solution:
In class A, 20 students passed in first class out of 25 students.
∴ Fraction of students getting first class

In class B, 24 students passed in first class out of 30 students.
∴ Fraction of students getting first class

Comparing the two fractions, we get 45 = 45
Hence, both the class A and B have the same fractions.

Fractions Class 6 Ex 7.5

Ex 7.5 Class 6 Maths Question 1.
Write these fractions appropriately as additions or subtractions.

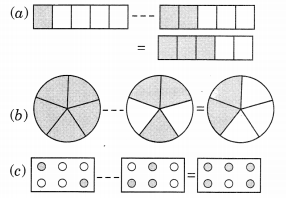
Solution:
(a) The given figure represents the addition of

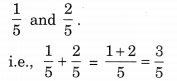
Thus the given diagrams can be represented as

(b) The given figure represents the difference between 1 and 35.

Thus, the given diagrams can be represented as

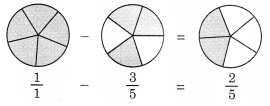
(c) The given figure represents addition of 26 and 36.

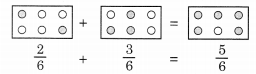
Thus, the given diagrams can be represented as

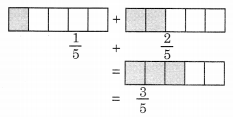
Ex 7.5 Class 6 Maths Question 2.
Solve:

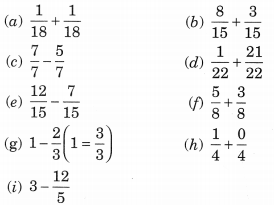
Solution:

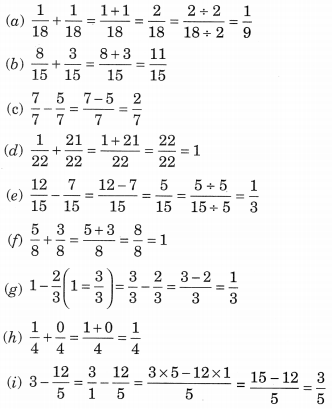
Ex 7.5 Class 6 Maths Question 3.
Shubham painted 23 of the wall space in his room. His sister Madhavi helped and painted 13 of the wall space. How much did they paint together?
Solution:
Fraction of wall painted by Shubham = 23
Fraction of wall painted by Madhavi = 13
Fraction of wall painted by Shubham and Madhavi

Thus the fraction of wall painted by both = 1

Ex 7.5 Class 6 Maths Question 4.
Fill in the missing fractions.

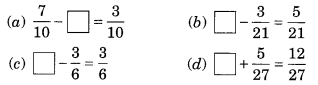
Solution:

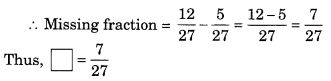
Ex 7.5 Class 6 Maths Question 5.
Javed was given 57 of a basket of oranges. What fraction of oranges was left in the basket?
Solution:
Fraction of basket of oranges = 57
Fraction of basket as a whole can be taken as 1.
∴ Fraction of basket of oranges left

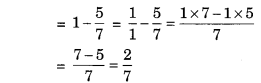
Thus, the required fraction = 27 .

Fractions Class 6 Ex 7.6

Ex 7.6 Class 6 Maths Question 1.
Solve


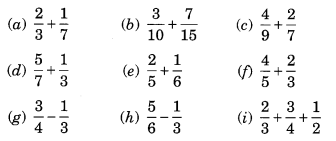
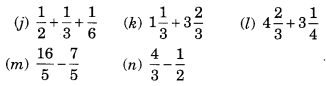
Solution:





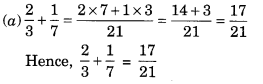
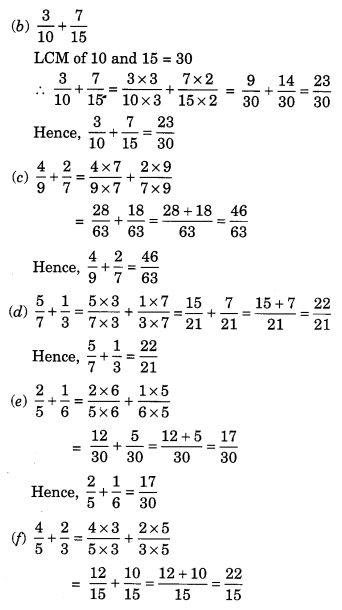
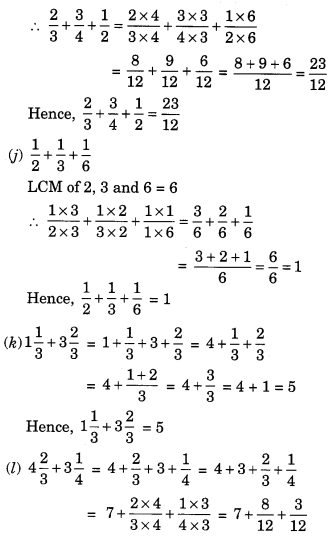
Ex 7.6 Class 6 Maths Question 2.
Sarita bought 25 metre of ribbon and Lalita 34 metre of ribbon. What is the total length of the ribbon they bought?
Solution:
Length of ribbon bought by Sarita = 25 metre
Length of ribbon bought by Lalita = 34 metre
∴ Length of ribbon bought by Sarita and Lalita

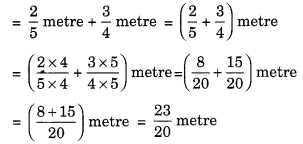
Hence, the required length = 2320 metre

Ex 7.6 Class 6 Maths Question 3.
Naina was given 112 piece of cake and Najma was given 113 piece of cake. Find the total amount of cake was given to both of them.
Solution:
Piece of cake given to Naina = 1112
Piece of cake given to Najma = 1113
Piece of cake given to Naina and Najma

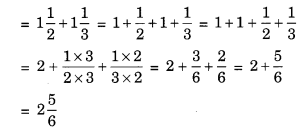
Hence the total amount of piece given to both = 256.

Ex 7.6 Class 6 Maths Question 4.
Fill in the boxes:

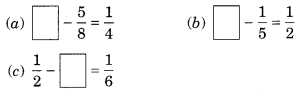
Solution:

Here, missing number is 14 more than 58 .


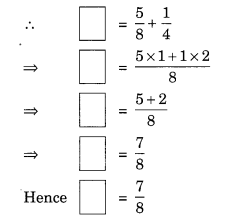
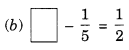
Here, missing number is 12 more than 15 .

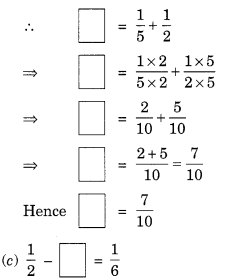
Here, missing number is 16 less than 12.

Ex 7.6 Class 6 Maths Question 5.
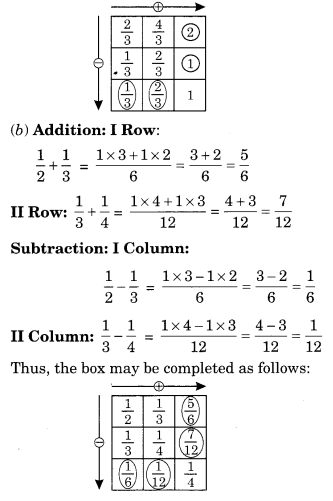
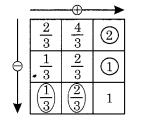
Complete the addition-subtraction box.

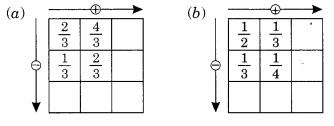
Solution:

Thus the box may be completed as follows:

Ex 7.6 Class 6 Maths Question 6.
A piece of wire 78 metre long broke into two pieces. One piece was 14 metre long. How long is the other piece?
Solution:
Total length of the wire = 78 metre
Length of one piece of wire = 14 metre
∴ Length of the other piece = 78 – 14
LCM of 8 and 4 = 8

Hence, the length of the other piece = 58 metre.

Ex 7.6 Class 6 Maths Question 7.
Nandini’s house is 910 km from her school. She walked some distance and then took a bus for 12km to reach the school. How far did she walk?
Solution:
Total distance from house to school = 910 km.
Distance travelled by Nandini by bus = 12 km
∴ Distance travelled by her on foot

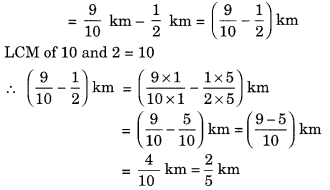
Hence, the distance travelled by her on foot = 25km.

Ex 7.6 Class 6 Maths Question 8.
Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is 56 th full and Samuel’s shelf is 25 th full. Whose bookshelf is more full? By what fraction?
Solution:
Asha’s shelf is 56 th full
and Samuel’s shelf is 25 th full
Comparing 56 and 25
LCM of 6 and 5 = 30

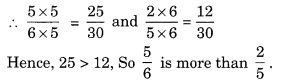
Hence, Asha’s shelf is full more than Samuel’s shelf.

Hence, 1330 th fraction is more full of Asha’s shelf.

Ex 7.6 Class 6 Maths Question 9.
Jaidev takes 215 minutes to walk across the school ground. Rahul takes 74 minutes to do the same. Who takes less time and by what fraction?
Solution:
Jaidev takes 215 minutes 5
Rahul takes 274 minutes
Comparing 215 minutes and 74 minutes


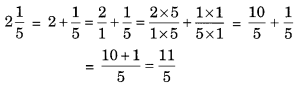
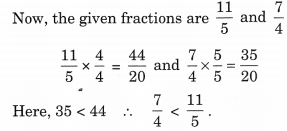
So, the time take to cover the same distance by Rahul is less than that of Jaidev.

Hence, Rahul takes 920 minutes less to across the school ground.