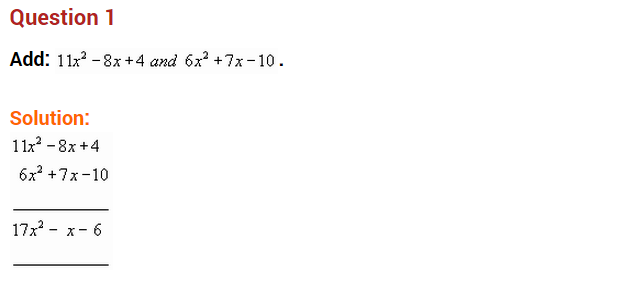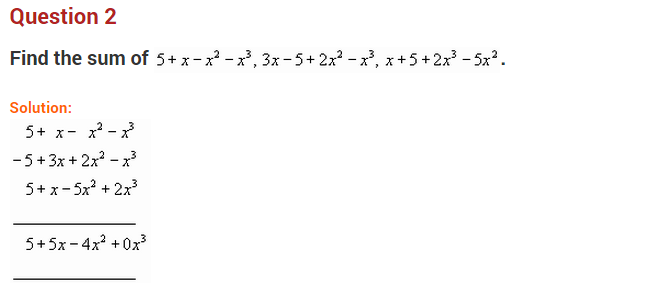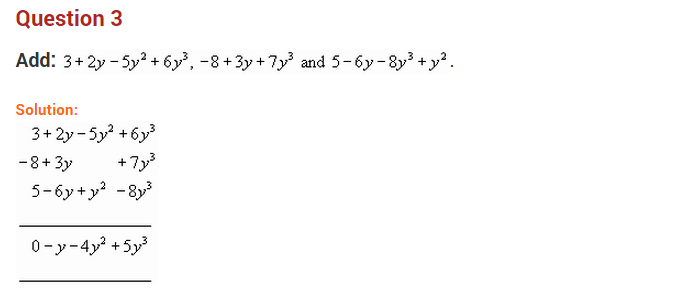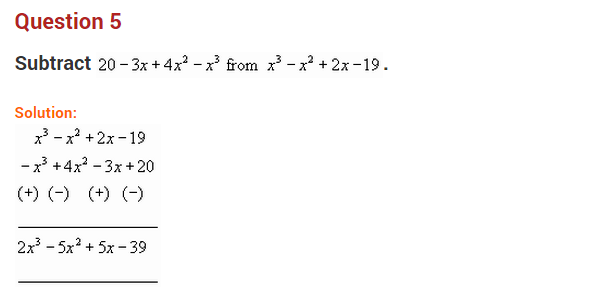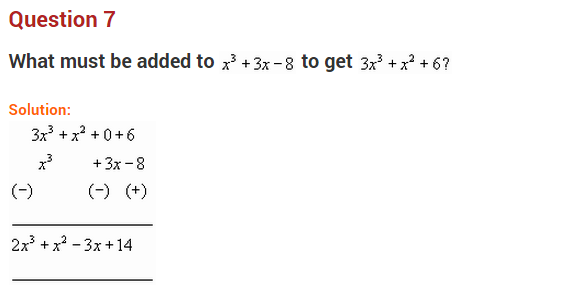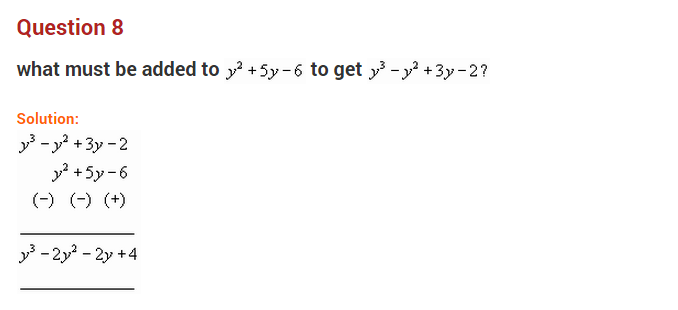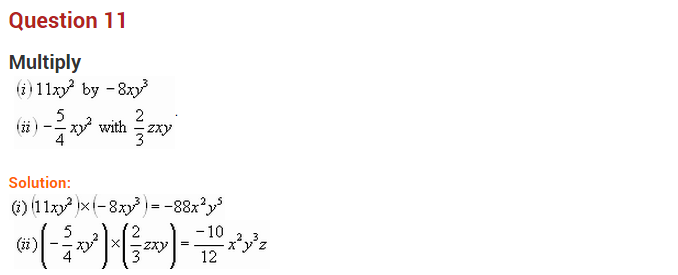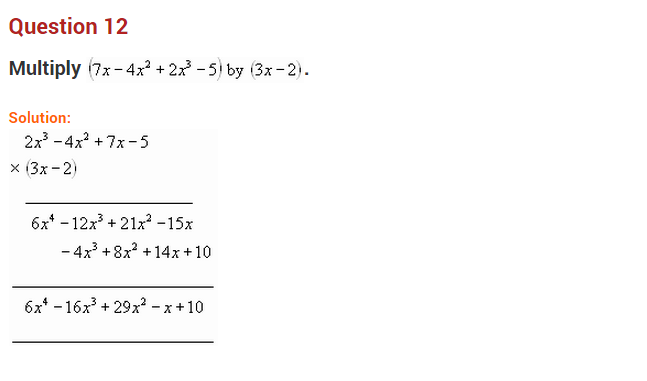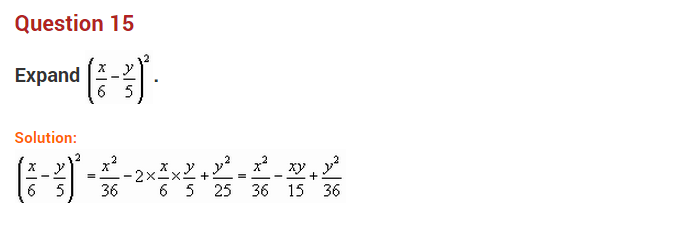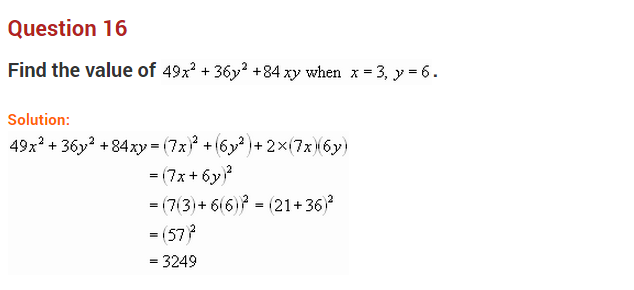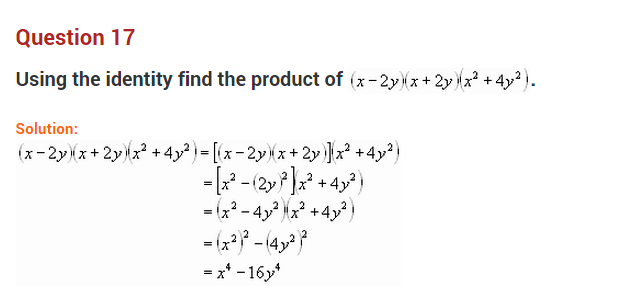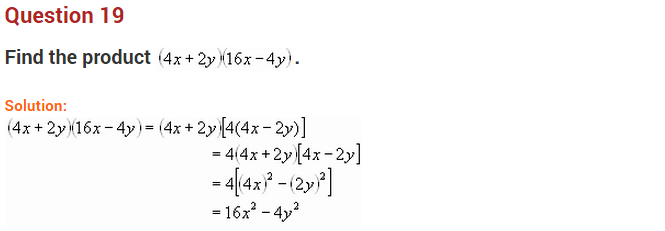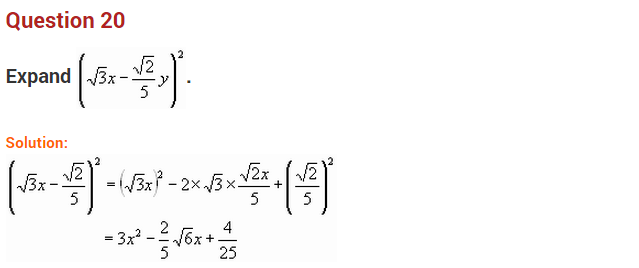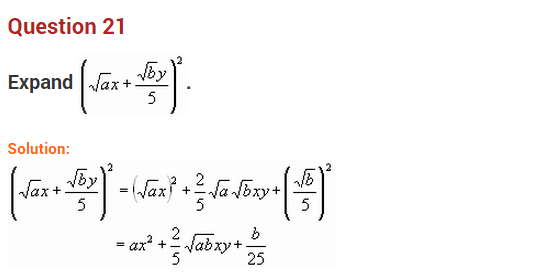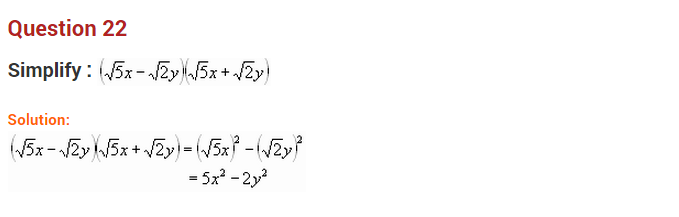NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.1

Ex 9.1 Class 8 Maths Question 1.
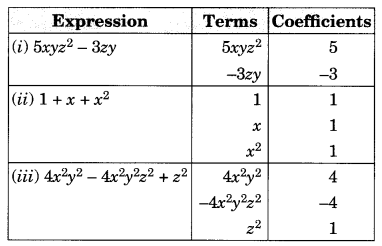
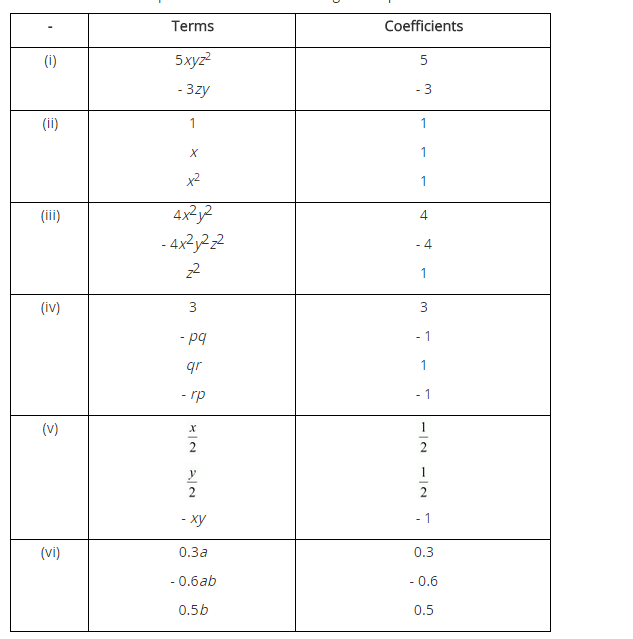
Identify the terms, their coefficients for each of the following expressions.
(i) 5xyz² – 3zy
(ii) 1 + x + x²
(iii) 4x²y² – 4x²y²z² + z²
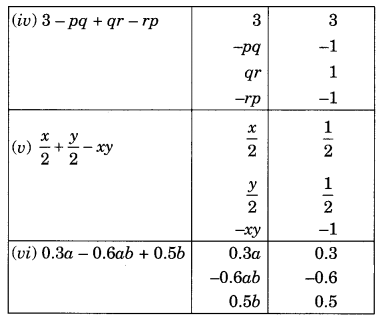
(iv) 3 – pq + qr – rp
(v) x2 + y2 – xy
(vi) 0.3a – 0.6ab + 0.5b
Solution:

Ex 9.1 Class 8 Maths Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x² + x³ + x⁴, 7 + y + 5x, 2y – 3y², 2y – 3y² + 4y³, 5x – 4y + 3xy, 4z – 15z², ab + bc + cd + da, pqr, p²q + pq², 2p + 2q
Solution:

Ex 9.1 Class 8 Maths Question 3.
Add the following:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²
(iv) l² + m², m² + n², n² + l², 2lm + 2mn + 2nl
Solution:
(i) Given: ab – bc, bc – ca, ca – ab
We have
(ab – bc) + (bc – ca) + (ca – ab) (Adding all the terms)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (Collecting the like terms together)
= 0 + 0 + 0
= 0

(ii) Given:
a – b + ab, b – c + bc, c – a + ac
We have (a – b + ab) + (b – c + bc) + (c – a + ac) (Adding all the terms)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (Collecting all the like terms together)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac

(iii) Given:
2p²q² – 3pq + 4, 5 + 7pq – 3p²q²
By arranging the like terms in the same column, we have

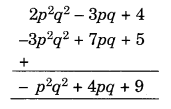
(Adding columnwise)

(iv) Given: l² + m², m² + n², n² + l², 2lm + 2mn + nl
By arranging the like terms in the same column, we have

Thus, the sum of the given expressions is 2(l² + m² + n² + lm + mn + nl)

Ex 9.1 Class 8 Maths Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(6) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq² + 5p²q
Solution:
(a) Arranging the like terms column-wise, we have

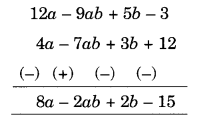
[Change the signs of all the terms of lower expressions and then add]
(b) Arranging the like terms column-wise, we have

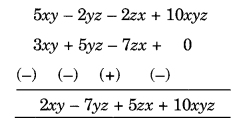
[Change the signs of all the terms of lower expressions and then add]
(c) Arranging the like terms column-wise, we have

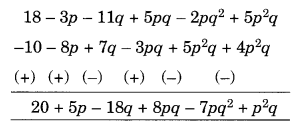
[Change the signs of all the terms of lower expressions and then add]
The terms are p²q – 7pq² + 8pq – 18q + 5p + 20

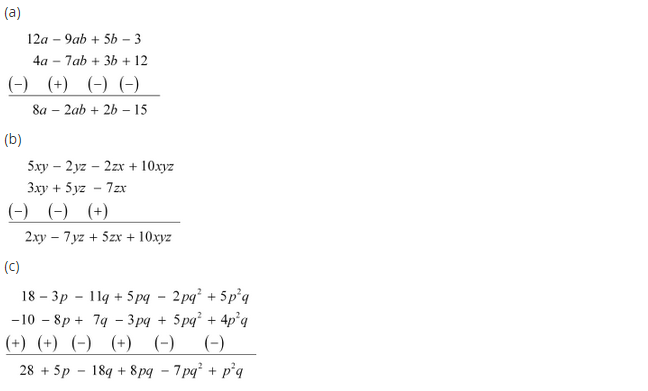
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.2

Ex 9.2 Class 8 Maths Question 1.
Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p³, -3p
(v) 4p, 0
Solution:
(i) 4 × 7p = (4 × 7) × p = 28p
(ii) -4p × 7p = (-4 × 7) × p × p = -28p²
(iii) -4p × 7pq = (-4 × 7) × p × pq = -28p²q
(iv) 4p³ × -3p = (4 × -3) × p³ × p = -12p⁴
(v) 4p x 0 = (4 × 0) × p = 0 × p = 0

Ex 9.2 Class 8 Maths Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
Solution:
(i) Length = p units and breadth = q units
Area of the rectangle = length × breadth = p × q = pq sq units
(ii) Length = 10 m units, breadth = 5n units
Area of the rectangle = length × breadth = 10 m × 5 n = (10 × 5) × m × n = 50 mn sq units
(iii) Length = 20x² units, breadth = 5y² units
Area of the rectangle = length × breadth = 20x² × 5y² = (20 × 5) × x² × y² = 100x²y² sq units
(iv) Length = 4x units, breadth = 3x² units
Area of the rectangle = length × breadth = 4x × 3x² = (4 × 3) × x × x² = 12x³ sq units
(v) Length = 3mn units, breadth = 4np units
Area of the rectangle = length × breadth = 3mn × 4np = (3 × 4) × mn × np = 12mn²p sq units

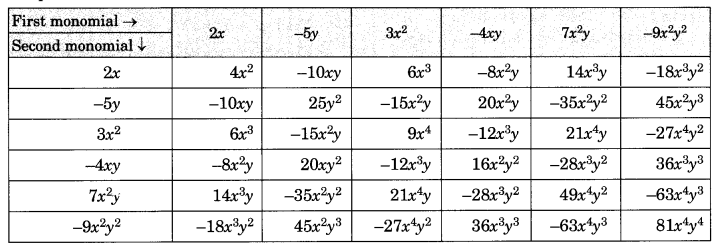
Ex 9.2 Class 8 Maths Question 3.
Complete the table of Products.

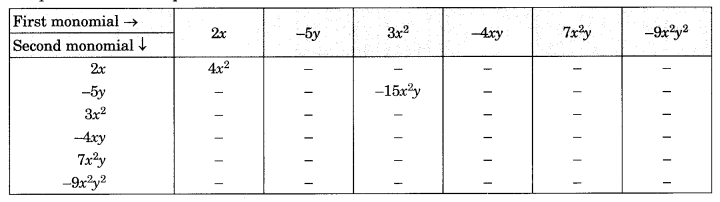
Solution:
Completed Table

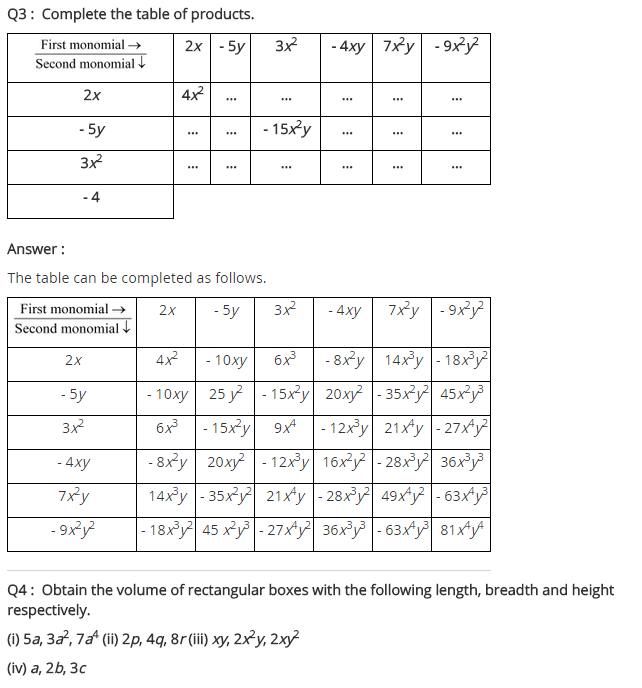
Ex 9.2 Class 8 Maths Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a², 7a⁴
(ii) 2p, 4q, 8r
(iii) xy, 2x²y, 2xy²
(iv) a, 2b, 3c
Solution:
(i) Here, length = 5a, breadth = 3a², height = 7a⁴
Volume of the box = l × b × h = 5a × 3a² × 7a⁴ = 105 a⁷ cu. units
(ii) Here, length = 2p, breadth = 4q, height = 8r
Volume of the box = l × b × h = 2p × 4q × 8r = 64pqr cu. units
(iii) Here, length = xy, breadth = 2x²y, height = 2xy²
Volume of the box = l × b × h = xy × 2x²y × 2xy² = (1 × 2 × 2) × xy × x²y × xy² = 4x⁴y⁴ cu. units
(iv) Here, length = a, breadth = 2b, height = 3c
Volume of the box = length × breadth × height = a × 2b × 3c = (1 × 2 × 3)abc = 6 abc cu. units

Ex 9.2 Class 8 Maths Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a, -a², a³
(iii) 2, 4y, 8y², 16y³
(iv) a, 2b, 3c, 6abc
(v) m, -mn, mnp
Solution:
(i) xy × yz × zx = x²y²z²
(ii) a × (-a²) × a³ = -a⁶
(iii) 2 × 4y × 8y² × 16y³ = (2 × 4 × 8 × 16) × y × y² × y³ = 1024y⁶
(iv) a × 2b × 3c × 6abc = (1 × 2 × 3 × 6) × a × b × c × abc = 36 a²b²c²
(v) m × (-mn) × mnp = [1 × (-1) × 1 ]m × mn × mnp = -m³n²p

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.3

Ex 9.3 Class 8 Maths Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a²b²
(iv) a² – 9, 4a
(v) pq + qr + rp, 0
Solution:
(i) 4p × (q + r) = (4p × q) + (4p × r) = 4pq + 4pr
(ii) ab, a – b = ab × (a – b) = (ab × a) – (ab × b) = a²b – ab²
(iii) (a + b) × 7a²b² = (a × 7a²b²) + (b × 7a²b²) = 7a³b² + 7a²b³
(iv) (a² – 9) × 4a = (a² × 4a) – (9 × 4a) = 4a³ – 36a
(v) (pq + qr + rp) × 0 = 0
[∵ Any number multiplied by 0 is = 0]

Ex 9.3 Class 8 Maths Question 2.
Complete the table.

S.No.	First Expression	Second Expression	Product
(i)	a	b + c + d	–
(ii)	x + y – 5	5xy	–
(iii)	p	6p2 – 7p + 5	–
(iv)	4p2q2	p2 – q2	–
(v)	a + b + c	abc	–

Solution:
(i) a × (b + c + d) = (a × b) + (a × c) + (a × d) = ab + ac + ad
(ii) (x + y – 5) (5xy) = (x × 5xy) + (y × 5xy) – (5 × 5xy) = 5x²y + 5xy² – 25xy
(iii) p × (6p² – 7p + 5) = (p × 6p²) – (p × 7p) + (p × 5) = 6p³ – 7p² + 5p
(iv) 4p²q² × (p² – q²) = 4p²q² × p² – 4p²q² × q² = 4p⁴q² – 4p²q⁴
(v) (a + b + c) × (abc) = (a × abc) + (b × abc) + (c × abc) = a²bc + ab²c + abc²

Completed Table:

S.No.	First Expression	Second Expression	Product
(i)	a	b + c + d	ab + ac + ad
(ii)	x + y – 5	5xy	5x2y + 5xy2 – 25xy
(iii)	p	6p2 – 7p + 5	6p3 – 7p2 + 5p
(iv)	4p2q2	p2 – q2	4p4q2 – 4p2q4
(v)	a + b + c	abc	a2bc + ab2c + abc2

Ex 9.3 Class 8 Maths Question 3.
Find the products.

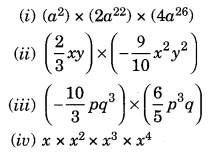
Solution:

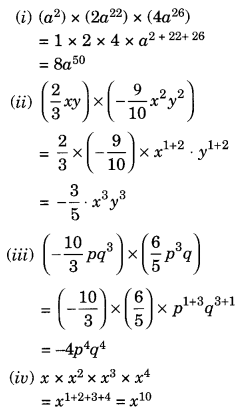
Ex 9.3 Class 8 Maths Question 4.
(a) Simplify: 3x(4x – 5) + 3 and find its values for (i) x = 3 (ii) x = 12.
(b) Simplify: a(a² + a + 1) + 5 and find its value for (i) a = 0 (ii) a = 1 (iii) a = -1
Solution:
(a) We have 3x(4x – 5) + 3 = 4x × 3x – 5 × 3x + 3 = 12x² – 15x + 3
(i) For x = 3, we have
12 × (3)² – 15 × 3 + 3 = 12 × 9 – 45 + 3 = 108 – 42 = 66

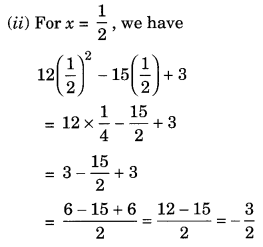
(b) We have a(a² + a + 1) + 5
= (a² × a) + (a × a) + (1 × a) + 5
= a³ + a² + a + 5
(i) For a = 0, we have
= (0)³ + (0)² + (0) + 5 = 5
(ii) For a = 1, we have
= (1)³ + (1)² + (1) + 5 = 1 + 1 + 1 + 5 = 8
(iii) For a = -1, we have
= (-1)³ + (-1)² + (-1) + 5 = -1 + 1 – 1 + 5 = 4

Ex 9.3 Class 8 Maths Question 5.
(a) Add: p(p – q), q(q – r) and r(r – p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l – 4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) p(p – q) + q(q – r) + r(r – p)
= (p × p) – (p × q) + (q × q) – (q × r) + (r × r) – (r × p)
= p² – pq + q² – qr + r² – rp
= p² + q² + r² – pq – qr – rp
(b) 2x(z – x – y) + 2y(z – y – x)
= (2x × z) – (2x × x) – (2x × y) + (2y × z) – (2y × y) – (2y × x)
= 2xz – 2x² – 2xy + 2yz – 2y² – 2xy
= -2x² – 2y² + 2xz + 2yz – 4xy
= -2x² – 2y² – 4xy + 2yz + 2xz
(c) 4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
= (4l × 10n) – (4l × 3m) + (4l × 2l) – (3l × l) – (3l × -4m) – (3l × 5n)
= 40ln – 12lm + 8l² – 3l² + 12lm – 15ln
= (40ln – 15ln) + (-12lm + 12lm) + (8l² – 3l²)
= 25ln + 0 + 5l²
= 25ln + 5l²
= 5l² + 25ln
(d) [4c(-a + b + c)] – [3a(a + b + c) – 2b(a – b + c)]
= (-4ac + 4bc + 4c²) – (3a² + 3ab + 3ac – 2ab + 2b² – 2bc)
= -4ac + 4bc + 4c² – 3a² – 3ab – 3ac + 2ab – 2b² + 2bc
= -3a² – 2b² + 4c² – ab + 6bc – 7ac

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.4

Ex 9.4 Class 8 Maths Question 1.
Multiply the binomials:
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q²) and (3pq – 2q²)
(vi) (34a² + 3b²) and 4(a² – 23 b²)
Solution:
(i) (2x + 5) × (4x – 3)
= 2x × (4x – 3) + 5 × (4x – 3)
= (2x × 4x) – (3 × 2x) + (5 × 4x) – (5 × 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15

(ii) (y – 8) × (3y – 4)
= y × (3y – 4) – 8 × (3y – 4)
= (y × 3y) – (y × 4) – (8 × 3y) + (-8 × -4)
= 3y² – 4y – 24y + 32
= 3y² – 28y + 32

(iii) (2.5l – 0.5m) × (2.5l + 0.5m)
= (2.5l × 2.5l) + (2.5l × 0.5m) – (0.5m × 2.5l) – (0.5m × 0.5m)
= 6.25l² + 1.25ml – 1.25ml – 0.25m²
= 6.25l² + 0 – 0.25m²
= 6.25l² – 0.25m²

(iv) (a + 3b) × (x + 5)
= a × (x + 5) + 36 × (x + 5)
= (a × x) + (a × 5) + (36 × x) + (36 × 5)
= ax + 5a + 3bx + 15b

(v) (2pq + 3q²) × (3pq – 2q²)
= 2pq × (3pq – 2q²) + 3q² (3pq – 2q²)
= (2pq × 3pq) – (2pq × 2q²) + (3q² × 3pq) – (3q² × 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6p²q² + 5pq³ – 6q⁴

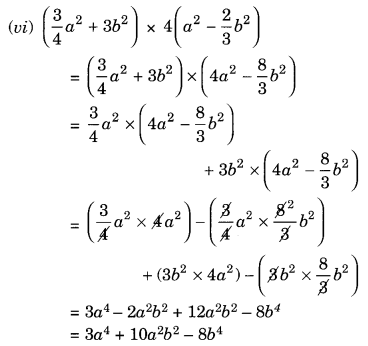
Ex 9.4 Class 8 Maths Question 2.
Find the product:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x – y)
(iii) (a² + b) (a + b²)
(iv) (p² – q²)(2p + q)
Solution:
(i) (5 – 2x) (3 + x)
= 5(3 + x) – 2x(3 + x)
= (5 × 3) + (5 × x) – (2x × 3) – (2x × x)
= 15 + 5x – 6x – 2x²

(ii) (x + 7y) (7x – y)
= x(7x – y) + 7y(7x – y)
= (x × 7x) – (x × y) + (7y × 7x) – (7y × y)
= 7x² – xy + 49xy – 7y²
= 7x² + 48xy – 7y²

(iii) (a² + b) (a + b²)
= a² (a + b²) + b(a + b²)
= (a² × a) + (a² × b²) + (b × a) + (b × b²)
= a³ + a²b² + ab + b³

(iv) (p² – q²)(2p + q)
= p²(2p + q) – q²(2p + q)
= (p² × 2p) + (p² × q) – (q² × 2p) – (q² × q)
= 2p³ + p²q – 2pq² – q³

Ex 9.4 Class 8 Maths Question 3.
Simplify:
(i) (x² – 5) (x + 5) + 25
(ii) (a² + 5)(b³ + 3) + 5
(iii) (t + s²) (t² – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2(ac + bd)
(v) (x + y) (2x + y) + (x + 2y) (x – y)
(vi) (x + y)(x² – xy + y²)
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c) (a + b – c)
Solution:
(i) (x² – 5) (x + 5) + 25
= x²(x + 5) + 5(x + 5) + 25
= x³ + 5x² – 5x – 25 + 25
= x³ + 5x² – 5x + 0
= x³ + 5x² – 5x

(ii) (a² + 5)(b³ + 3) + 5
= a²(b³ + 3) + 5(b³ + 3) + 5
= a²b³ + 3a² + 5b³ + 15 + 5
= a²b³ + 3a² + 5b³ + 20

(iii) (t + s²) (t² – s)
= t(t² – s) + s²(t² – s)
= t³ – st + s²t² – s³
= t³ + s²t² – st – s³

(iv) (a + b)(c – d) + (a – b) (c + d) + 2(ac + bd)
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2ac + 2bd
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= ac + ac + 2ac + bc – bc – ad + ad – bd – bd + 2bd
= 4ac + 0 + 0 + 0
= 4ac

(v) (x + y) (2x + y) + (x + 2y) (x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= 2x² + x² + xy + 2xy – xy + 2xy + y² – 2y²
= 3x² + 4xy – y²

(vi) (x + y)(x² – xy + y²)
= x(x² – xy + y²) + y(x² – xy + y²)
= x³ – x²y + x²y + xy² – xy² + y³
= x³ – 0 + 0 + y³
= x³ + y³

(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x.+ 12y
= 1.5x (1.5x + 4y + 3) – 4y(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 6xy + 4.5x – 6xy – 16y² – 12y – 4.5x + 12y
= 2.25x² + 6xy – 6xy + 4.5x – 4.5x + 12y – 12y – 16y²
= 2.25x² + 0 + 0 + 0 – 16y²
= 2.25x² – 16y²

(viii) (a + b + c) (a + b – c)
= a(a + b – c) + b(a + b – c) + c(a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + ab + ab – bc + bc – ac + ac + b² – c²
= a² + 2ab + b² – c² + 0 + 0
= a² + 2ab + b² – c²

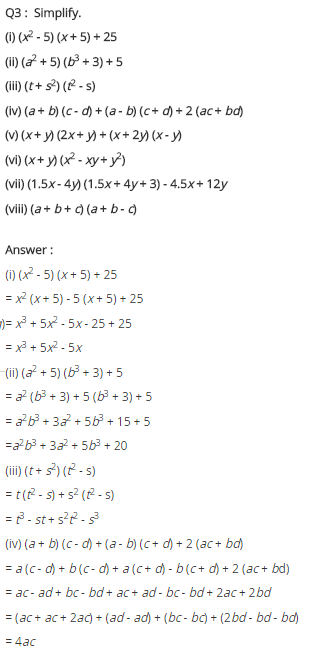
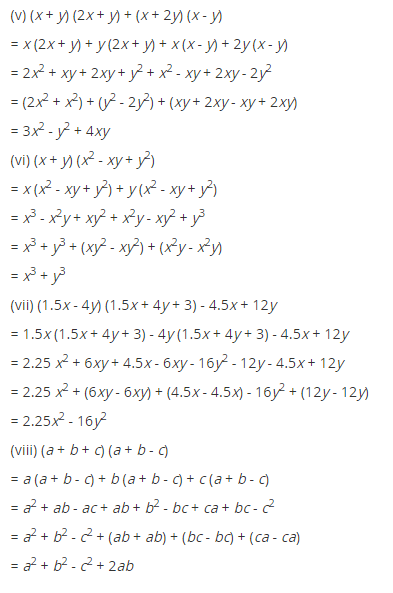
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.5

Ex 9.5 Class 8 Maths Question 1.
Use a suitable identity to get each of the following products:
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv) (3a – 12) (3a – 12)
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a² + b²) (-a² + b²)
(vii) (6x – 7) (6x + 7)
(viii) (-a + c) (-a + c)
(ix) (x2 + 3y4) (x2 + 3y4)
(x) (7a – 9b) (7a – 9b)
Solution:

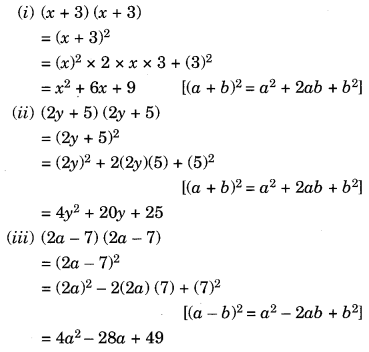
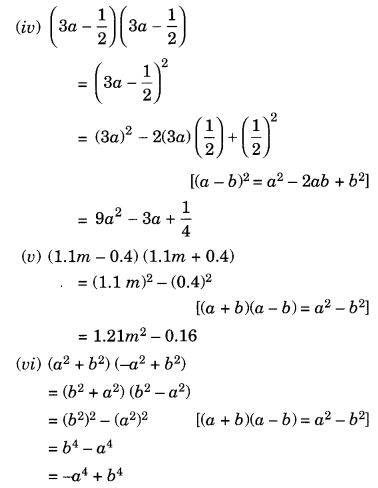
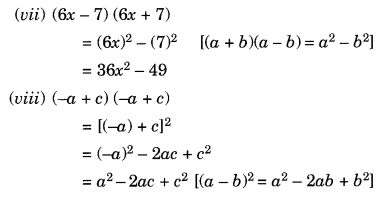
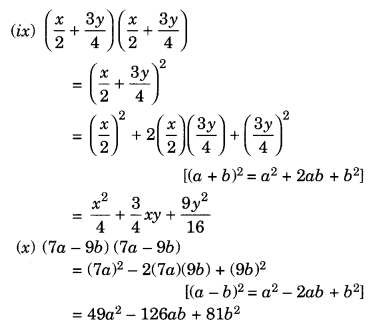
Ex 9.5 Class 8 Maths Question 2.
Use the identity (x + a)(x + b) = x² + (a + b)x + ab to find the following products.
(i) (x + 3) (x + 7)
(ii) (4x + 5)(4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a² + 9) (2a² + 5)
(vii) (xyz – 4) (xyz – 2)
Solution:

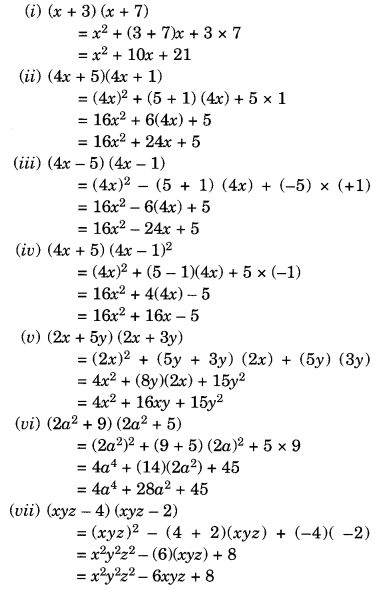
Ex 9.5 Class 8 Maths Question 3.
Find the following squares by using the identities.
(i) (b – 7)²
(ii) (xy + 3z)²
(iii) (6x² – 5y)²
(iv) (23 m + 32 n)²
(v) (0.4p – 0.5q)²
(vi) (2xy + 5y)²
Solution:

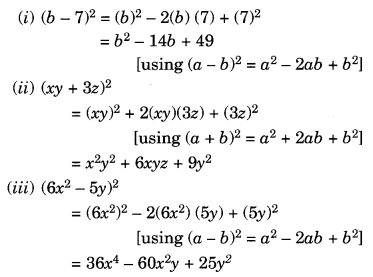
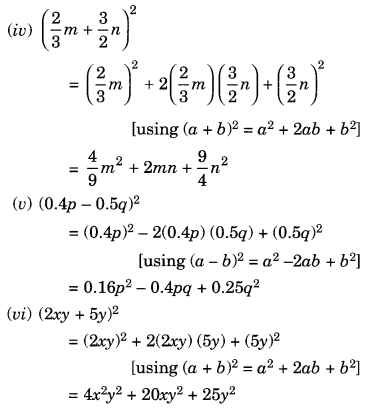
Ex 9.5 Class 8 Maths Question 4.
Simplify:
(i) (a² – b²)²
(ii) (2x + 5)² – (2x – 5)²
(iii) (7m – 8n)² + (7m + 8n)²
(iv) (4m + 5n)² + (5m + 4n)²
(v) (2.5p – 1.5q)² – (1.5p – 2.5q)²
(vi) (ab + bc)² – 2ab²c
(vii) (m² – n²m)² + 2m³n²
Solution:

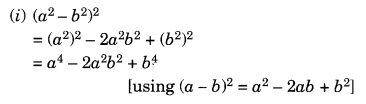
Ex 9.5 Class 8 Maths Question 5.
Show that:
(i) (3x + 7)² – 84x = (3x – 7)²
(ii) (9p – 5q)² + 180pq = (9p + 5q)²
(iii) (43 m – 34 n)² + 2mn = 169 m² + 916 n²
(iv) (4pq + 3q)² – (4pq – 3q)² = 48pq²
(v) (a – b)(a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
Solution:

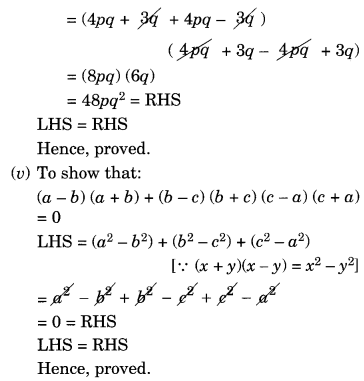
Ex 9.5 Class 8 Maths Question 6.
Using identities, evaluate:
(i) 71²
(ii) 99²
(iii) 102²
(iv) 998²
(v) 5.2²
(vi) 297 × 303
(vii) 78 × 82
(viii) 8.9²
(ix) 1.05 × 9.5
Solution:

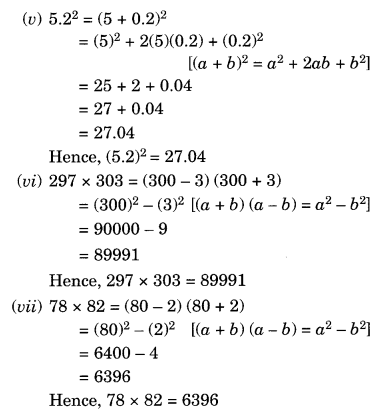
Ex 9.5 Class 8 Maths Question 7.
Using a² – b² = (a + b) (a – b), find
(i) 51² – 49²
(ii) (1.02)² – (0.98)²
(iii) 153² – 147²
(iv) 12.1² – 7.9²
Solution:
(i) 51² – 49² = (51 + 49) (51 – 49) = 100 × 2 = 200
(ii) (1.02)² – (0.98)² = (1.02 + 0.98) (1.02 – 0.98) = 2.00 × 0.04 = 0.08
(iii) 153² – 147² = (153 + 147) (153 – 147) = 300 × 6 = 1800
(iv) 12.1² – 7.9² = (12.1 + 7.9) (12.1 – 7.9) = 20.0 × 4.2 = 84

Ex 9.5 Class 8 Maths Question 8.
Using (x + a) (x + b) = x² + (a + b)x + ab, find
(i) 103 × 104
(ii) 5.1 × 5.2
(iii) 103 × 98
(iv) 9.7 × 9.8
Solution:
(i) 103 × 104 = (100 + 3)(100 + 4) = (100)² + (3 + 4) (100) + 3 × 4 = 10000 + 700 + 12 = 10712
(ii) 5.1 × 5.2 = (5 + 0.1) (5 + 0.2) = (5)² + (0.1 + 0.2) (5) + 0.1 × 0.2 = 25 + 1.5 + 0.02 = 26.5 + 0.02 = 26.52
(iii) 103 × 98 = (100 + 3) (100 – 2) = (100)² + (3 – 2) (100) + 3 × (-2) = 10000 + 100 – 6 = 10100 – 6 = 10094
(iv) 9.7 × 9.8 = (10 – 0.3) (10 – 0.2) = (10)² – (0.3 + 0.2) (10) + (-0.3) (-0.2) = 100 – 5 + 0.06 = 95 + 0.06 = 95.06

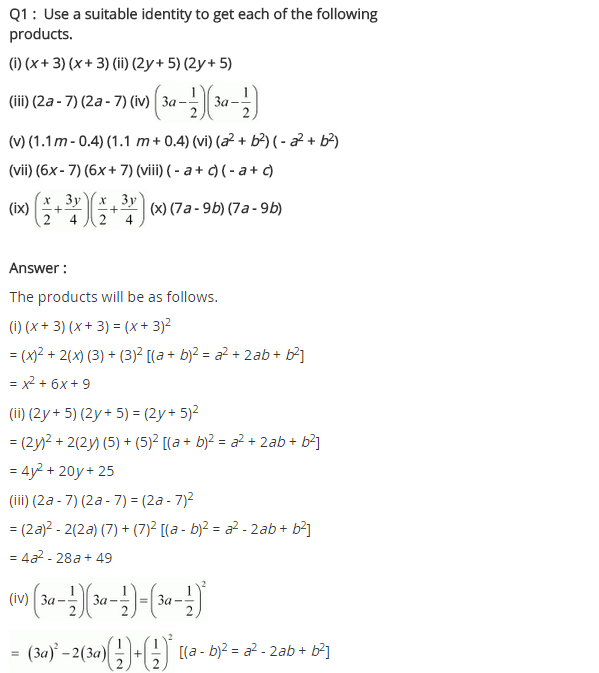
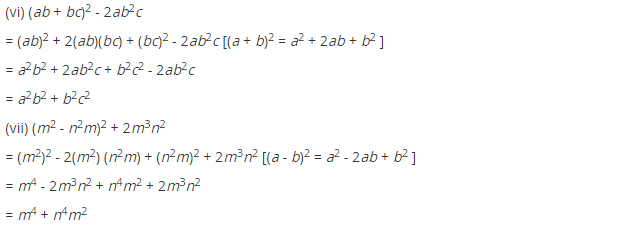
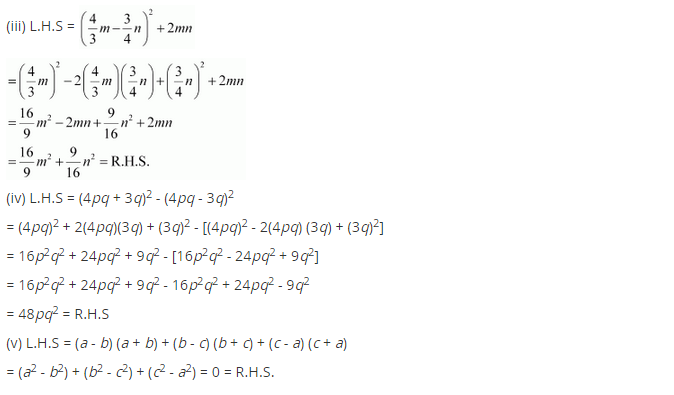
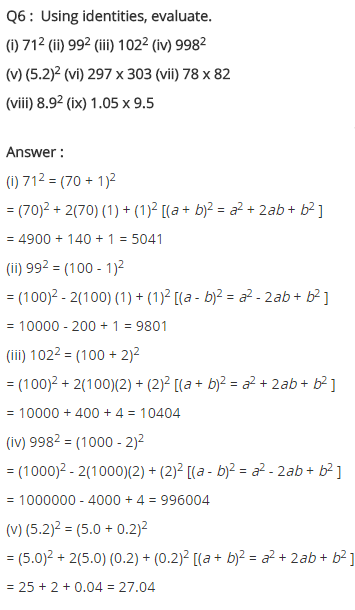
Algebraic Expressions and Identities Class 8 Extra Questions Maths Chapter 9

Extra Questions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities

Algebraic Expressions and Identities Class 8 Extra Questions Very Short Answer Type

Question 1.
Write two examples of each of
(i) Monomials
(ii) Binomials
(iii) Trinomials
Solution:
(i) Monomials:
(a) 3x
(b) 5xy²
(ii) Binomials:
(a) p + q
(b) -5a + 2b
(iii) Trinomials:
(a) a + b + c
(b) x² + x + 2

Question 2.
Identify the like expressions.
5x, -14x, 3x² + 1, x², -9x², xy, -3xy
Solution:
Like terms: 5x and -14x, x² and -9x², xy and -3xy

Question 3.
Identify the terms and their coefficients for each of the following expressions:
(i) 3x²y – 5x
(ii) xyz – 2y
(iii) -x – x²
Solution:

Question 4.
Add: -3a²b², –52 a²b², 4a²b², 23 a²b²
Solution:

Question 5.
Add: 8x² + 7xy – 6y², 4x² – 3xy + 2y² and -4x² + xy – y²
Solution:

Question 6.
Subtract: (4x + 5) from (-3x + 7)
Solution:
(-3x + 7) – (4x + 5) = -3x + 7 – 4x – 5 = -3x – 4x + 7 – 5 = -7x + 2

Question 7.
Subtract: 3x² – 5x + 7 from 5x² – 7x + 9
Solution:
(5x² – 7x + 9) – (3x² – 5x + 7)
= 5x² – 7x + 9 – 3x² + 5x – 7
= 5x² – 3x² + 5x – 7x + 9 – 7
= 2x² – 2x + 2

Question 8.
Multiply the following expressions:
(a) 3xy² × (-5x²y)
(b) 12 x²yz × 23 xy²z × 15 x²yz
Solution:

Question 9.
Find the area of the rectangle whose length and breadths are 3x²y m and 5xy² m respectively.
Solution:
Length = 3x²y m, breadth = 5xy² m
Area of rectangle = Length × Breadth = (3x²y × 5xy²) sq m = (3 × 5) × x²y × xy² sq m = 15x³y³ sq m

Question 10.
Multiply x² + 7x – 8 by -2y.
Solution:

Algebraic Expressions and Identities Class 8 Extra Questions Short Answer Type

Question 11.
Simplify the following:
(i) a² (b² – c²) + b² (c² – a²) + c² (a² – b²)
(ii) x²(x – 3y²) – xy(y² – 2xy) – x(y³ – 5x²)
Solution:
(i) a² (b² – c²) + b² (c² – a²) + c² (a² – b²)
= a²b² – a²c²) + b²c² – b²a²) + c²a² – c²b²)
= 0
(ii) x²(x – 3y²) – xy(y² – 2xy) – x(y³ – 5x²)
= x³ – 3x²y² – xy³ + 2x²y² – xy³ + 5x³
= x³ + 5x³ – 3x²y² + 2x²y² – xy³ – xy³
= 6x³ – x²y² – 2xy³

Question 12.
Multiply (3x² + 5y²) by (5x² – 3y²)
Solution:
(3x² + 5y²) × (5x² – 3y²)
= 3x²(5x² – 3y²) + 5y²(5x² – 3y²)
= 15x⁴ – 9x²y² + 25x²y² – 15y⁴
= 15x⁴ + 16x²y² – 15y⁴

Question 13.
Multiply (6x² – 5x + 3) by (3x² + 7x – 3)
Solution:
(6x² – 5x + 3) × (3x² + 7x – 3)
= 6x²(3x² + 7x – 3) – 5x(3x² + 7x – 3) + 3(3x² + 7x – 3)
= 18x⁴ + 42x³ – 18x² – 15x³ – 35x² + 15x + 9x² + 21x – 9
= 18x⁴ + 42x³ – 15x³ – 18x² – 35x² + 9x² + 15x + 21x – 9
= 18x⁴ + 27x³ – 44x² + 36x – 9

Question 14.
Simplify:
2x²(x + 2) – 3x (x² – 3) – 5x(x + 5)
Solution:
2x²(x + 2) – 3x(x² – 3) – 5x(x + 5)
= 2x³ + 4x² – 3x³ + 9x – 5x² – 25x
= 2x³ – 3x³ – 5x² + 4x² + 9x – 25x
= -x³ – x² – 16x

Question 15.
Multiply x² + 2y by x³ – 2xy + y³ and find the value of the product for x = 1 and y = -1.
Solution:
(x² + 2y) × (x³ – 2xy + y³)
= x²(x³ – 2xy + y³) + 2y(x³ – 2xy + y³)
= x⁵ – 2x³y + x²y³ + 2x³y – 4xy² + 2y⁴
= x⁵ + x²y³ – 4xy² + 2y⁴
Put x = 1 and y = -1
= (1)⁵ + (1)² (-1)³ – 4(1)(-1)² + 2(-1)⁴
= 1 + (1) (-1) – 4(1)(1) + 2(1)
= 1 – 1 – 4 + 2
= -2

Question 16.
Using suitable identity find:
(i) 48² (NCERT Exemplar)
(ii) 96²
(iii) 231² – 131²
(iv) 97 × 103
(v) 181² – 19² = 162 × 200 (NCERT Exemplar)
Solution:

Question 17.

Solution:

Question 18.
Verify that (11pq + 4q)² – (11pq – 4q)² = 176pq² (NCERT Exemplar)
Solution:
LHS = (11pq + 4q)² – (11pq – 4q)² = (11pq + 4q + 11pq – 4q) × (11pq + 4q – 11pq + 4q)
[using a² -b² = (a – b) (a + b), here a = 11pq + 4q and b = 11 pq – 4q]
= (22pq) (8q)
= 176 pq²
= RHS.
Hence Verified.

Question 19.
Find the value of 382−22216, using a suitable identity. (NCERT Exemplar)
Solution:

Question 20.
Find the value of x, if 10000x = (9982)² – (18)² (NCERT Exemplar)
Solution:
RHS = (9982)² – (18)² = (9982 + 18)(9982 – 18)
[Since a² -b² = (a + b) (a – b)]
= (10000) × (9964)
LHS = (10000) × x
Comparing L.H.S. and RHS, we get
10000x = 10000 × 9964
x = 9964