NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.1

Ex 14.1 Class 8 Maths Question 1.
Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14pq, 28p²q²
(iv) 2x, 3x², 4
(v) 6abc, 24ab², 12a²b
(vi) 16x³, -4x², 32x
(vii) 10pq, 20qr, 30rp
(viii) 3x²y³, 10x³y², 6x²y²z
Solution:
(i) 12x, 36
(2 × 2 × 3 × x) and (2 × 2 × 3 × 3)
Common factors are 2 × 2 × 3 = 12
Hence, the common factor = 12

(ii) 2y, 22xy
= (2 × y) and (2 × 11 × x × y)
Common factors are 2 × y = 2y
Hence, the common factor = 2y

(iii) 14pq, 28p²q²
= (2 × 7 × p × q) and (2 × 2 × 7 × p × p × q × q)
Common factors are 2 × 7 × p × q = 14pq
Hence, the common factor = 14pq

(iv) 2x, 3x², 4
= (2 × x), (3 × x × x) and (2 × 2)
Common factor is 1
Hence, the common factor = 1 [∵ 1 is a factor of every number]

(v) 6abc, 24ab², 12a²b
= (2 × 3 × a × b × c), (2 × 2 × 2 × 3 × a × b × b) and (2 × 2 × 3 × a × a × b)
Common factors are 2 × 3 × a × b = 6ab
Hence, the common factor = 6ab

(vi) 16x³, -4x², 32x
= (2 × 2 × 2 × 2 × x × x × x), -(2 × 2 × x × x), (2 × 2 × 2 × 2 × 2 × x)
Common factors are 2 × 2 × x = 4x
Hence, the common factor = 4x

(vii) 10pq, 20qr, 30rp
= (2 × 5 × p × q), (2 × 2 × 5 × q × r), (2 × 3 × 5 × r × p)
Common factors are 2 × 5 = 10
Hence, the common factor = 10

(viii) 3x²y², 10x³y², 6x²y²z
= (3 × x × x × y × y), (2 × 5 × x × x × x × y × y), (2 × 3 × x × x × y × y × z)
Common factors are x × x × y × y = x²y²
Hence, the common factor = x²y².

Ex 14.1 Class 8 Maths Question 2.
Factorise the following expressions.
(i) 7x – 42
(ii) 6p – 12q
(iii) 7a² + 14a
(iv) -16z + 20z³
(v) 20l²m + 30alm
(vi) 5x²y – 15xy²
(vii) 10a² – 15b² + 20c²
(viii) -4a² + 4ab – 4ca
(ix) x²yz + xy²z + xyz²
(x) ax²y + bxy² + cxyz
Solution:
(i) 7x – 42 = 7(x – 6)
(ii) 6p – 12q = 6(p – 2q)
(iii) 7a² + 14a = 7a(a + 2)
(iv) -16z + 20z³ = 4z(-4 + 5z²)
(v) 20l²m + 30alm = 10lm(2l + 3a)
(vi) 5x²y – 15xy² = 5xy(x – 3y)
(vii) 10a² – 15b² + 20c² = 5(2a² – 3b² + 4c²)
(viii) -4a² + 4ab – 4ca = 4a(-a + b – c)
(ix) x²yz + xy²z + xyz² = xyz(x + y + z)
(x) ax²y + bxy² + cxyz = xy(ax + by + cz)

Ex 14.1 Class 8 Maths Question 3.
Factorise:
(i) x² + xy + 8x + 8y
(ii) 15xy – 6x + 5y – 2
(iii) ax + bx – ay – by
(iv) 15pq + 15 + 9q + 25p
(v) z – 7 + 7xy – xyz
Solution:
(i) x² + xy + 8x + 8y
Grouping the terms, we have
x² + xy + 8x + 8y
= x(x + y) + 8(x + y)
= (x + y)(x + 8)
Hence, the required factors = (x + y)(x + 8)

(ii) 15xy – 6x + 5y – 2
Grouping the terms, we have
(15xy – 6x) + (5y – 2)
= 3x(5y – 2) + (5y – 2)
= (5y – 2)(3x + 1)

(iii) ax + bx – ay – by
Grouping the terms, we have
= (ax – ay) + (bx – by)
= a(x – y) + b(x – y)
= (x – y)(a + b)
Hence, the required factors = (x – y)(a + b)

(iv) 15pq + 15 + 9q + 25p
Grouping the terms, we have
= (15pq + 25p) + (9q + 15)
= 5p(3q + 5) + 3(3q + 5)
= (3q + 5) (5p + 3)
Hence, the required factors = (3q + 5) (5p + 3)

(v) z – 7 + 7xy – xyz
Grouping the terms, we have
= (-xyz + 7xy) + (z – 7)
= -xy(z – 7) + 1 (z – 7)
= (-xy + 1) (z – 1)
Hence the required factor = -(1 – xy) (z – 7)

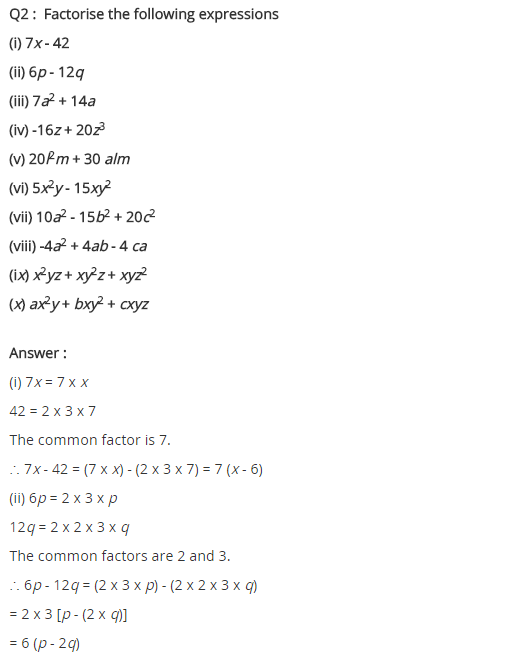
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.2

Ex 14.2 Class 8 Maths Question 1.
Factorise the following expressions.
(i) a² + 8a +16
(ii) p² – 10p + 25
(iii) 25m² + 30m + 9
(iv) 49y² + 84yz + 36z²
(v) 4x² – 8x + 4
(vi) 121b² – 88bc + 16c²
(vii) (l + m)² – 4lm. (Hint: Expand (l + m)² first)
(viii) a⁴ + 2a²b² + b⁴
Solution:
(i) a² + 8a + 16
Here, 4 + 4 = 8 and 4 × 4 = 16
a² + 8a +16
= a² + 4a + 4a + 4 × 4
= (a² + 4a) + (4a + 16)
= a(a + 4) + 4(a + 4)
= (a + 4) (a + 4)
= (a + 4)²

(ii) p² – 10p + 25
Here, 5 + 5 = 10 and 5 × 5 = 25
p² – 10p + 25
= p² – 5p – 5p + 5 × 5
= (p² – 5p) + (-5p + 25)
= p(p – 5) – 5(p – 5)
= (p – 5) (p – 5)
= (p – 5)²

(iii) 25m² + 30m + 9
Here, 15 + 15 = 30 and 15 × 15 = 25 × 9 = 225
25m² + 30m + 9
= 25m² + 15m + 15m + 9
= (25m² + 15m) + (15m + 9)
= 5m(5m + 3) + 3(5m + 3)
= (5m + 3) (5m + 3)
= (5m + 3)²

(iv) 49y² + 84yz + 36z²
Here, 42 + 42 = 84 and 42 × 42 = 49 × 36 = 1764
49y² + 84yz + 36z²
= 49y² + 42yz + 42yz + 36z²
= 7y(7y + 6z) +6z(7y + 6z)
= (7y + 6z) (7y + 6z)
= (7y + 6z)²

(v) 4x² – 8x + 4
= 4(x² – 2x + 1) [Taking 4 common]
= 4(x² – x – x + 1)
= 4[x(x – 1) -1(x – 1)]
= 4(x – 1)(x – 1)
= 4(x – 1)²

(vi) 121b² – 88bc + 16c²
Here, 44 + 44 = 88 and 44 × 44 = 121 × 16 = 1936
121b² – 88bc + 16c²
= 121b² – 44bc – 44bc + 16c²
= 11b(11b – 4c) – 4c(11b – 4c)
= (11b – 4c) (11b – 4c)
= (11b – 4c)²

(vii) (l + m)² – 4lm
Expanding (l + m)², we get
l² + 2lm + m² – 4lm
= l² – 2lm + m²
= l² – Im – lm + m²
= l(l – m) – m(l – m)
= (l – m) (l – m)
= (l – m)²

(viii) a⁴ + 2a²b² + b⁴
= a⁴ + a²b² + a²b² + b⁴
= a²(a² + b²) + b²(a² + b²)
= (a² + b²)(a² + b²)
= (a² + b²)²

Ex 14.2 Class 8 Maths Question 2.
Factorise.
(i) 4p² – 9q²
(ii) 63a² – 112b²
(iii) 49x² – 36
(iv) 16x⁵ – 144x³
(v) (l + m)² – (l – m)²
(vi) 9x²y² – 16
(vii) (x² – 2xy + y²) – z²
(viii) 25a² – 4b² + 28bc – 49c²
Solution:
(i) 4p² – 9q²
= (2p)² – (3q)²
= (2p – 3q) (2p + 3q)
[∵ a² – b² = (a + b)(a – b)]

(ii) 63a² – 112b²
= 7(9a² – 16b²)
= 7 [(3a)² – (4b)²]
= 7(3a – 4b)(3a + 4b)
[∵ a² – b² = (a + b)(a – b)]

(iii) 49x² – 36 = (7x)² – (6)²
= (7x – 6) (7x + 6)
[∵ a² – b² = (a + b)(a – b)]

(iv) 16x⁵ – 144x³ = 16x³ (x² – 9)
= 16x³ [(x)² – (3)²]
= 16x³(x – 3)(x + 3)
[∵ a² – b² = (a + b)(a – b)]

(v) (l + m)² – (l – m)²
= (l + m) – (l – m)] [(l + m) + (l – m)]
[∵ a² – b² = (a + b)(a – b)]
= (l + m – l + m)(l + m + l – m)
= (2m) (2l)
= 4ml

(vi) 9x²y² – 16 = (3xy)² – (4)²
= (3xy – 4)(3xy + 4)
[∵ a² – b² = (a + b)(a – b)]

(vii) (x² – 2xy + y²) – z²
= (x – y)² – z²
= (x – y – z) (x – y + z)
[∵ a² – b² = (a + b)(a – b)]

(viii) 25a² – 4b² + 28bc – 49c²
= 25a² – (4b² – 28bc + 49c²)
= (5a)² – (2b – 7c)²
= [5a – (2b – 7c)] [5a + (2b – 7c)]
= (5a – 2b + 7c)(5a + 2b – 7c)

Ex 14.2 Class 8 Maths Question 3.
Factorise the expressions.
(i) ax² + bx
(ii) 7p² + 21q²
(iii) 2x³ + 2xy² + 2xz²
(iv) am² + bm² + bn² + an²
(v) (lm + l) + m + 1
(vi) y(y + z) + 9(y + z)
(vii) 5y² – 20y – 8z + 2yz
(viii) 10ab + 4a + 5b + 2
(ix) 6xy – 4y + 6 – 9x
Solution:
(i) ax² + bx = x(ax + 5)

(ii) 7p² + 21q² = 7(p² + 3q²)

(iii) 2x³ + 2xy² + 2xz² = 2x(x² + y² + z²)

(iv) am² + bm² + bn² + an²
= m² (a + b) + n²(a + b)
= (a + b)(m² + n²)

(v) (lm + l) + m + 1
= l(m + 1) + (m + 1)
= (m + 1) (l + 1)

(vi) y(y + z) + 9(y + z) = (y + z)(y + 9)

(vii) 5y² – 20y – 8z + 2yz
= 5y² – 20y + 2yz – 8z
= 5y(y – 4) + 2z(y – 4)
= (y – 4) (5y + 2z)

(viii) 10ab + 4a + 5b + 2
= 2a(5b + 2) + 1(5b + 2)
= (5b + 2)(2a + 1)

(ix) 6xy – 4y + 6 – 9x
= 6xy – 4y – 9x + 6
= 2y(3x – 2) – 3(3x – 2)
= (3x – 2) (2y – 3)

Ex 14.2 Class 8 Maths Question 4.
Factorise.
(i) a⁴ – b⁴
(ii) p⁴ – 81
(iii) x⁴ – (y + z)⁴
(iv) x⁴ – (x – z)⁴
(v) a⁴ – 2a²b² + b⁴
Solution:
(i) a⁴ – b⁴ – (a²)² – (b²)²
[∵ a² – b² = (a – b)(a + b)]
= (a² – b²) (a² + b²)
= (a – b) (a + b) (a² + b²)

(ii) p⁴ – 81 = (p²)² – (9)²
= (p² – 9) (p² + 9)
[∵ a² – b² = (a – b)(a + b)]
= (p – 3)(p + 3) (p² + 9)

(iii) x⁴ – (y + z)⁴ = (x²)² – [(y + z)²]²
[∵ a² – b² = (a – b)(a + b)]
= [x² – (y + z)²] [x² + (y + z)²]
= [x – (y + z)] [x + (y + z)] [x² + (y + z)²]
= (x – y – z) (x + y + z) [x² + (y + z)²]

(iv) x⁴ – (x – z)⁴ = (x²)² – [(y – z)²]²
= [x² – (y – z)²] [x² + (y – z)²]
= (x – y + z) (x + y – z) (x² + (y – z)²]

(v) a⁴ – 2a²b² + b⁴
= a⁴ – a²b² – a²b² + b⁴
= a²(a² – b²) – b²(a² – b²)
= (a² – b²)(a² – b²)
= (a² – b²)²
= [(a – b) (a + b)]²
= (a – b)² (a + b)²

Ex 14.2 Class 8 Maths Question 5.
Factorise the following expressions.
(i) p² + 6p + 8
(ii) q² – 10q + 21
(iii) p² + 6p – 16
Solution:
(i) p² + 6p + 8
Here, 2 + 4 = 6 and 2 × 4 = 8
p² + 6p + 8
= p² + 2p + 4p + 8
= p (p + 2) + 4(p + 2)
= (p + 2) (p + 4)

(ii) q² – 10q + 21
Here, 3 + 7 = 10 and 3 × 7 = 21
q² – 10q + 21
= q² – 3q – 7q + 21
= q(q – 3) – 7(q – 3)
= (q – 3) (q – 7)

(iii) p² + 6p – 16
Here, 8 – 2 = 6 and 8 × 2 = 16
p² + 6p – 16
= p² + 8p – 2p – 16
= p(p + 8) – 2(p + 8)
= (p + 8) (p – 2)

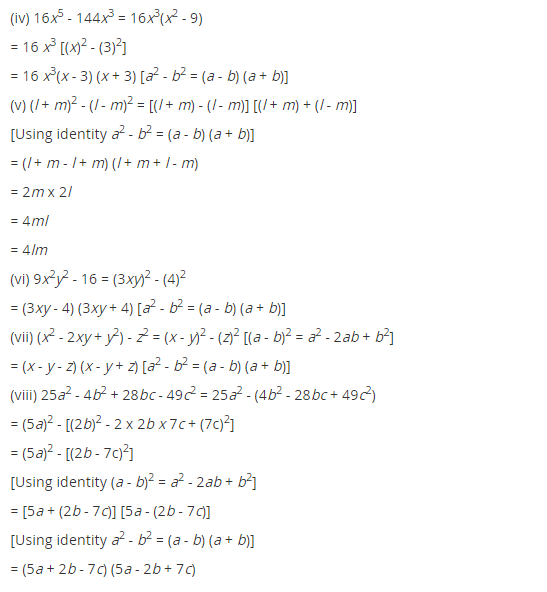
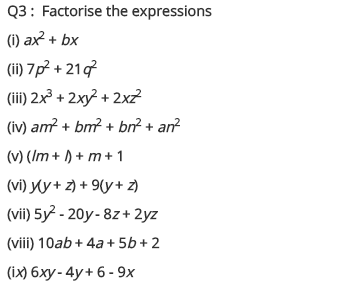
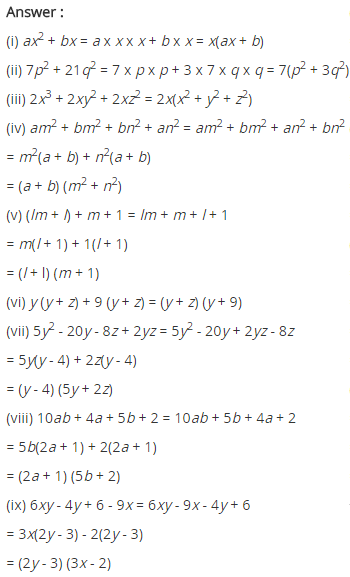
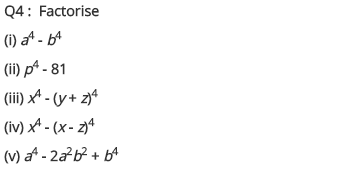
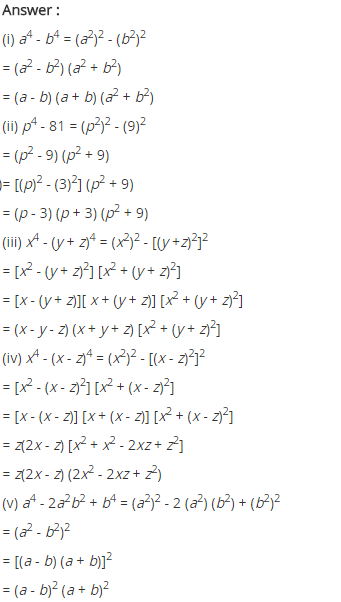
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.3

Ex 14.3 Class 8 Maths Question 1.
Carry out the following divisions.
(i) 28x⁴ ÷ 56x
(ii) -36y³ ÷ 9y²
(iii) 66pq²r³ ÷ 11qr²
(iv) 34x³y³z³ ÷ 51xy²z³
(v) 12a⁸b⁸ ÷ (-6a⁶b⁴)
Solution:

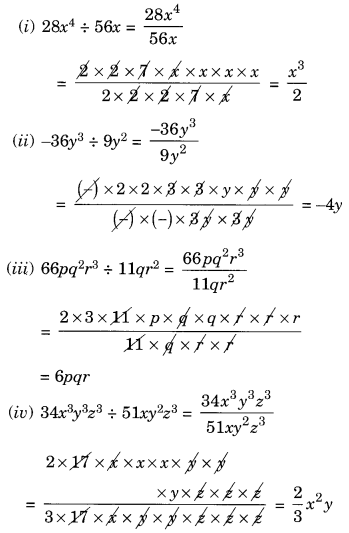
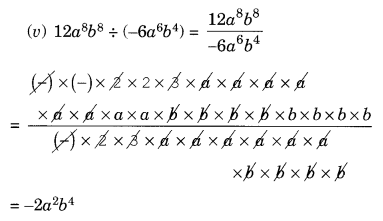
Ex 14.3 Class 8 Maths Question 2.
Divide the following polynomial by the given monomial.
(i) (5x² – 6x) ÷ 3x
(ii) (3y⁸ – 4y⁶ + 5y⁴) ÷ y⁴
(iii) 8(x³y²z² + x²y³z² + x²y²z³) ÷ 4x²y²z²
(iv) (x³ + 2x² + 3x) ÷ 2x
(v) (p³q⁶ – p⁶q³) ÷ p³q³
Solution:

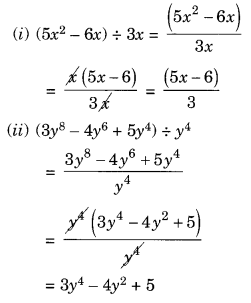
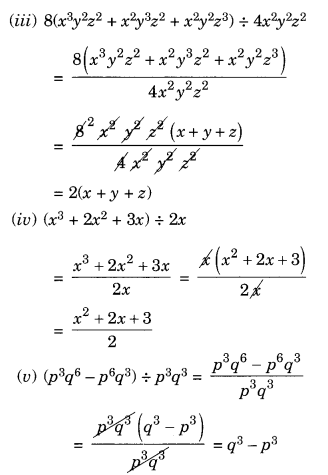
Ex 14.3 Class 8 Maths Question 3.
Work out the following divisions.
(i) (10x – 25) ÷ 5
(ii) (10x – 25) ÷ (2x – 5)
(iii) 10y(6y + 21) ÷ 5(2y + 7)
(iv) 9x²y²(3z – 24) ÷ 27xy(z – 8)
(v) 96abc(3a – 12) (5b – 30) ÷ 144(a – 4)(b – 6)
Solution:

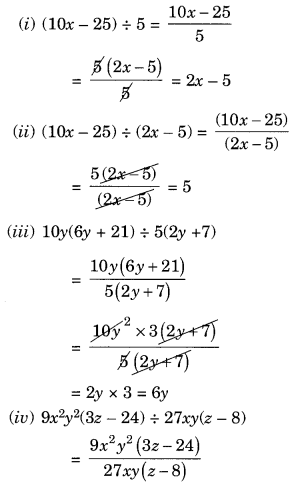
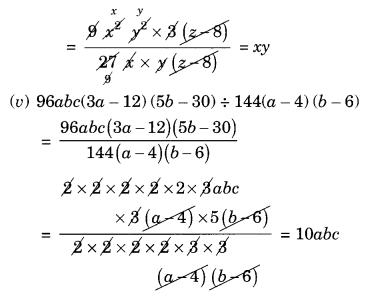
Ex 14.3 Class 8 Maths Question 4.
Divide as directed.
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)
(ii) 26xy (x + 5)(y – 4) ÷ 13x(y – 4)
(iii) 52pqr(p + q) (q + r) (r + p) ÷ 104pq(q + r)(r + p)
(iv) 20(y + 4)(y² + 5y + 3) ÷ 5(y + 4)
(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
Solution:

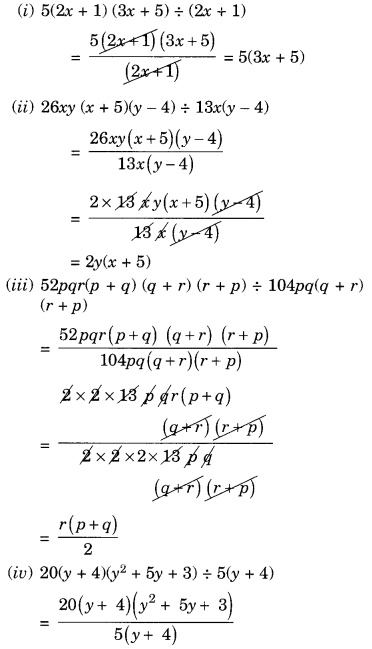
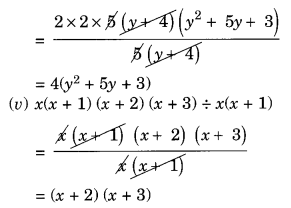
Ex 14.3 Class 8 Maths Question 5.
Factorise the expressions and divide them as directed.
(i) (y² + 7y + 10) ÷ (y + 5)
(ii) (m² – 14m – 32) ÷ (m + 2)
(iii) (5p² – 25p + 20) ÷ (p – 1)
(iv) 4yz(z² + 6z – 16) ÷ 2y(z + 8)
(v) 5pq(p² – q²) ÷ 2p(p + q)
(vi) 12xy(9x² – 16y²) ÷ 4xy(3x + 4y)
(vii) 39y³(50y² – 98) ÷ 26y²(5y + 7)
Solution:

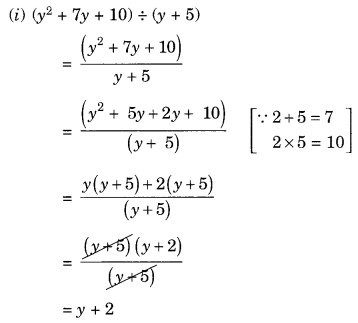
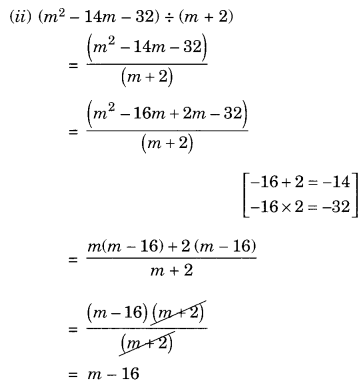
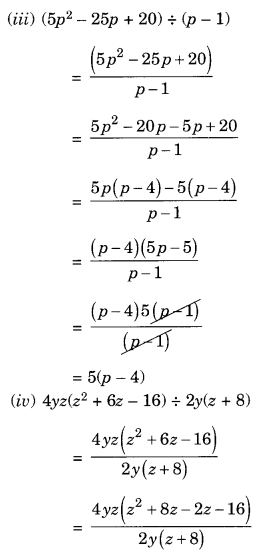
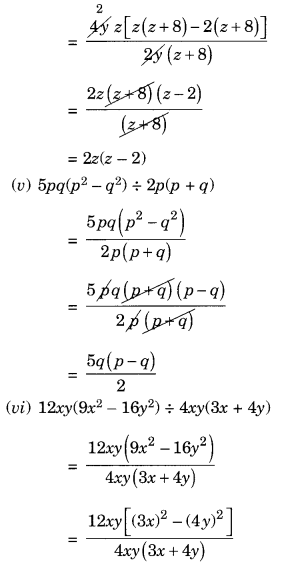
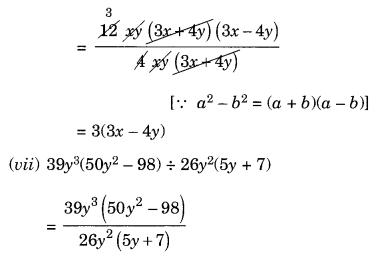
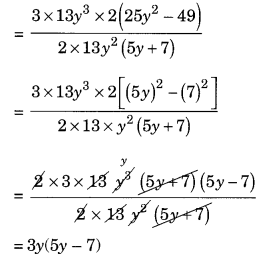
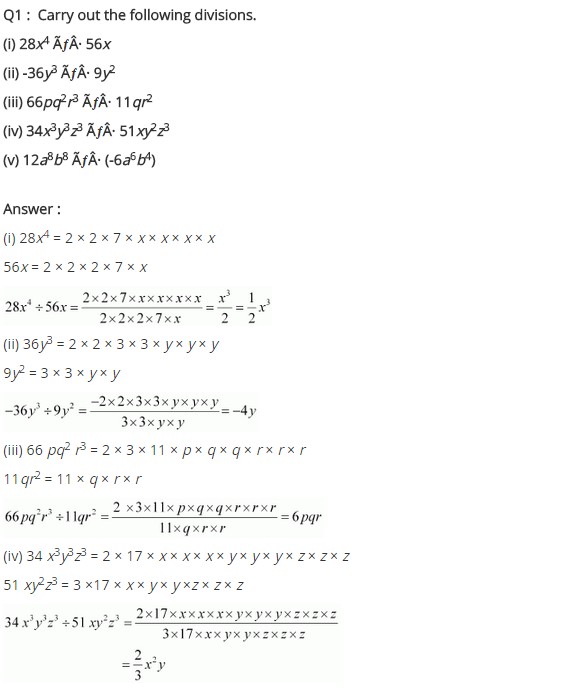
Factorisation Class 8 Extra Questions Maths Chapter 14

Extra Questions for Class 8 Maths Chapter 14 Factorisation

Factorisation Class 8 Extra Questions Very Short Answer Type

Question 1.
Find the common factors of the following terms.
(a) 25x²y, 30xy²
(b) 63m³n, 54mn⁴
Solution:
(a) 25x²y, 30xy²
25x²y = 5 × 5 × x × x × y
30xy² = 2 × 3 × 5 × x × y × y
Common factors are 5× x × y = 5 xy

(b) 63m³n, 54mn⁴
63m³n = 3 × 3 × 7 × m × m × m × n
54mn⁴ = 2 × 3 × 3 × 3 × m × n × n × n × n
Common factors are 3 × 3 × m × n = 9mn

Question 2.
Factorise the following expressions.
(a) 54m³n + 81m⁴n²
(b) 15x²y³z + 25x³y²z + 35x²y²z²
Solution:
(a) 54m³n + 81m⁴n²
= 2 × 3 × 3 × 3 × m × m × m × n + 3 × 3 × 3 × 3 × m × m × m × m × n × n
= 3 × 3 × 3 × m × m × m × n × (2 + 3 mn)
= 27m³n (2 + 3mn)

(b) 15x²y³z + 25 x³y²z + 35x²y²z² = 5x²y²z ( 3y + 5x + 7)

Question 3.
Factorise the following polynomials.
(a) 6p(p – 3) + 1 (p – 3)
(b) 14(3y – 5z)³ + 7(3y – 5z)²
Solution:
(a) 6p(p – 3) + 1 (p – 3) = (p – 3) (6p + 1)
(b) 14(3y – 5z)³ + 7(3y – 5z)²
= 7(3y – 5z)² [2(3y – 5z) +1]
= 7(3y – 5z)² (6y – 10z + 1)

Question 4.
Factorise the following:
(a) p²q – pr² – pq + r²
(b) x² + yz + xy + xz
Solution:
(a) p²q – pr² – pq + r²
= (p²q – pq) + (-pr² + r2)
= pq(p – 1) – r²(p – 1)
= (p – 1) (pq – r²)

(b) x² + yz + xy + xz
= x² + xy +xz + yz
= x(x + y) + z(x + y)
= (x + y) (x + z)

Question 5.
Factorise the following polynomials.
(a) xy(z² + 1) + z(x² + y²)
(b) 2axy² + 10x + 3ay² + 15
Solution:
(a) xy(z² + 1) + z(x² + y²)
= xyz² + xy + 2x² + zy²
= (xyz² + zx²) + (xy + zy²)
= zx(yz + x) + y(x + yz)
= zx(x + yz) + y(x + yz)
= (x + yz) (zx + y)

(b) 2axy² + 10x + 3ay² + 15
= (2axy² + 3ay²) + (10x + 15)
= ay²(2x + 3) +5(2x + 3)
= (2x + 3) (ay² + 5)

Question 6.
Factorise the following expressions.
(а) x² + 4x + 8y + 4xy + 4y²
(b) 4p² + 2q² + p²q² + 8
Solution:
(a) x² + 4x + 8y + 4xy + 4y²
= (x² + 4xy + 4y²) + (4x + 8y)
= (x + 2y)² + 4(x + 2y)
= (x + 2y)(x + 2y + 4)

(b) 4p² + 2q² + p²q² + 8
= (4p² + 8) + (p²q² + 2q²)
= 4(p² + 2) + q²(p² + 2)
= (p² + 2)(4 + q²)

Question 7.
Factorise:
(a) a² + 14a + 48
(b) m² – 10m – 56
Solution:
(a) a² + 14a + 48
= a² + 6a + 8a + 48
[6 + 8 = 14 ; 6 × 8 = 48]
= a(a + 6) + 8(a + 6)
= (a + 6) (a + 8)

(b) m² – 10m – 56
= m² – 14m + 4m – 56
[14 – 4 = 10; 4 × 4 = 56]
= m(m – 14) + 6(m – 14)
= (m – 14) (m + 6)

Question 8.
Factorise:
(a) x⁴ – (x – y)⁴
(b) 4x² + 9 – 12x – a² – b² + 2ab
Solution:
(a) x⁴ – (x – y)⁴
= (x²)² – [(x – y)²]²
= [x² – (x – y)²] [x² + (x – y)²]
= [x + (x – y] [x – (x – y)] [x² + x² – 2xy + y²]
= (x + x – y) (x – x + y)[2x² – 2xy + y²]
= (2x – y) y(2x² – 2xy + y²)
= y(2x – y) (2x² – 2xy + y²)

(b) 4x² + 9 – 12x – a² – b² + 2ab
= (4x² – 12x + 9) – (a² + b² – 2ab)
= (2x – 3)² – (a – b)²
= [(2x – 3) + (a – b)] [(2x – 3) – (a – b)]
= (2x – 3 + a – b)(2x – 3 – a + b)

Factorisation Class 8 Extra Questions Short Answer Type

Question 9.
Factorise the following polynomials.
(a) 16x⁴ – 81
(b) (a – b)² + 4ab
Solution:
(a) 16x⁴ – 81
= (4x²)² – (9)2
= (4x² + 9)(4x² – 9)
= (4x² + 9)[(2x)² – (3)²]
= (4x² + 9)(2x + 3) (2x – 3)

(b) (a – b)² + 4ab
= a² – 2ab + b² + 4ab
= a² + 2ab + b²
= (a + b)²

Question 10.
Factorise:
(а) 14m⁵n⁴p² – 42m⁷n³p⁷ – 70m⁶n⁴p³
(b) 2a²(b² – c²) + b²(2c² – 2a²) + 2c²(a² – b²)
Solution:
(a) 14m⁵n⁴p² – 42m⁷n³p⁷ – 70m⁶n⁴p³
= 14m⁵n³p²(n – 3m²p⁵ – 5mnp)

(b) 2a²(b² – c²) + b²(2c² – 2a²) + 2c²(a² – b²)
= 2a²(b² – c²) + 2b²(c² – a²) + 2c²(a² – b²)
= 2[a²(b² – c²) + b²(c² – a²) + c²(a² – b²)]

= 2 × 0
= 0

Question 11.
Factorise:
(a) (x + y)² – 4xy – 9z²
(b) 25x² – 4y² + 28yz – 49z²
Solution:
(a) (x + y)² – 4xy – 9z²
= x² + 2xy + y² – 4xy – 9z²
= (x² – 2xy + y²) – 9z²
= (x – y)² – (3z)²
= (x – y + 3z) (x – y – 3z)

(b) 25x² – 4y² + 28yz – 49z²
= 25x² – (4y² – 28yz + 49z²)
= (5x)² – (2y – 7)²
= (5x + 2y – 7) [5x – (2y – 7)]
= (5x + 2y – 7) (5x – 2y + 7)

Question 12.
Evaluate the following divisions:
(a) (3b – 6a) ÷ (30a – 15b)
(b) (4x² – 100) ÷ 6(x + 5)
Solution:

Question 13.
Simplify the following expressions:

Solution:

Question 14.
Factorise the given expressions and divide that as indicated.
(a) 39n³(50n² – 98 ) ÷ 26n²(5n – 7)
(b) 44(p⁴ – 5p³ – 24p²) ÷ 11p(p – 8)
Solution:

Question 15.
If one of the factors of (5x² + 70x – 160) is (x – 2). Find the other factor.
Solution:
Let the other factor be m.
(x – 2) × m = 5x² + 70x – 160