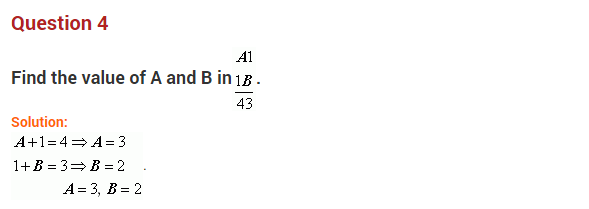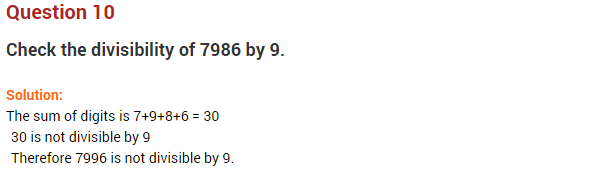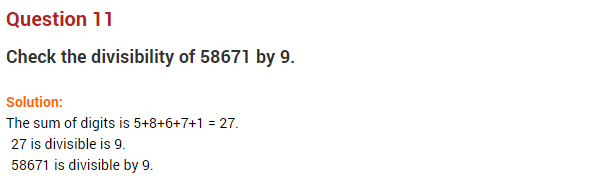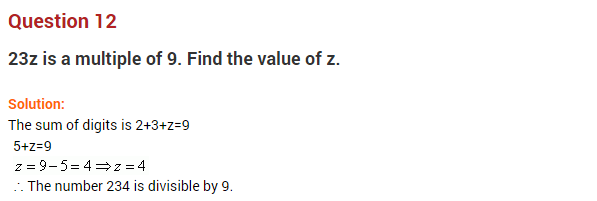NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Exercise 16.1

Find the values of the letters in each of the following and give reasons for the steps involved.
Ex 16.1 Class 8 Maths Question 1.

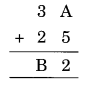
Solution:

Ex 16.1 Class 8 Maths Question 2.

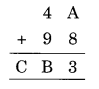
Solution:

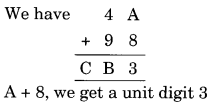
Ex 16.1 Class 8 Maths Question 3.

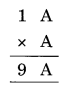
Solution:

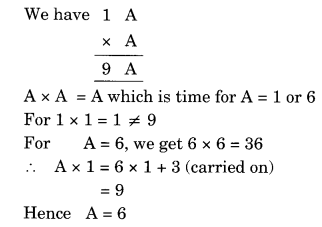
Ex 16.1 Class 8 Maths Question 4.

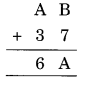
Solution:

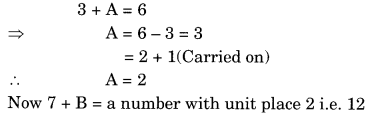
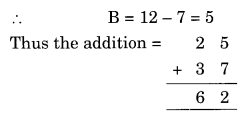
Ex 16.1 Class 8 Maths Question 5.

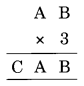
Solution:
3 × B = B
⇒ B = D
3 × A = CA
⇒ 3 × 5 = 15
Thus A = 5 and C = 1
Hence A = 5, B = 0 and C = 1

Ex 16.1 Class 8 Maths Question 6.

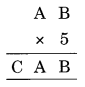
Solution:
5 × B = B
⇒ B = 0 or 5
5 × A = CA
5 × 5 = 25
Only possible when B = 0
Thus A = 5 and C = 2
Hence A = 5, B = 0 and C = 2

Ex 16.1 Class 8 Maths Question 7.

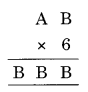
Solution:
B × 6 = B
6 × 4 = 24 → B = 4 and 2 is carried to
6 × A = BB
⇒ 6 × 7 = 42 + 2 (carried on) = 44
Thus B = 7
Hence A = 7 and B = 4

Ex 16.1 Class 8 Maths Question 8.

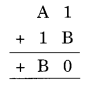
Solution:
1 + B = 0
1 + 9 = 10 → unit digit is 0 and 1 is carried to A
+ 1 +1 (carried on) = B = 9
A + 2 = 9 ⇒ A = 9 – 2 = 7
Hence A = 7 and B = 9

Ex 16.1 Class 8 Maths Question 9.

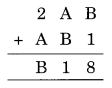
Solution:
B + 1 = 8 ⇒ B = 8 – 1 = 7
A + B = a number with unit digit 1
A + B = 11
⇒ A + 7 = 11
⇒ A = 11 – 7 = 4 (1 Carried to)
Now 1 carried on + 2 + A = B
3 + A = 7
⇒ A = 7 – 3 = 4
Hence A = 4, B = 7

Ex 16.1 Class 8 Maths Question 10.

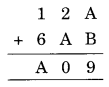
Solution:
9 = A + B
9 = 1 + 8 or 2 + 7 or 3 + 6 or 4 + 5 or 8 + 1 or 7 + 2 or 6 + 3 or 5 + 4 or 0 + 9 or 9 + 0
Now 0 is required at unit place
2 + A = 10
⇒ A = 10 – 2 = 8
B = 9 – 8 = 1
1 + 6 + 1 (carried on) = A = 8
Hence A = 8 and B = 1

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Exercise 16.2

Ex 16.2 Class 8 Maths Question 1.
If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
Solution:
A number is divisible by 9 if the sum of its digits is also divisible by 9.
Sum of the digits of 21y5 = 2 + 1 +y + 5 = 8 + y
(8 + y) ÷ 9 = 1
⇒ 8 + y = 9
⇒ y = 9 – 8 = 1
Hence, the required value of y = 1.

Ex 16.2 Class 8 Maths Question 2.
If 31z5 is a multiple of 9, where z is a digit, what is the value of z?
Solution:
A number is a multiple of 9 when the sum of its digits is also divisible by 9.
Sum of the digits of 31z5 = 3 + 1 + z + 5
3 + 1 + 2 + 5 = 9k where k is an integer.
For k = 1,
3 + 1 + z + 5 = 9
⇒ z = 9 – 9 = 0
For k = 2,
3 + 1 + z + 5 = 18
⇒ z = 18 – 9 = 9
k = 3 is not possible because 3 + 1 + z + 5 = 27
⇒ z = 27 – 9 = 18 which is not a digit.
Hence the required value of z is 0 or 9

Ex 16.2 Class 8 Maths Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x?
Solution:
Since 24x is a multiple of 3, the sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers; 0, 3, 6, 12, 15, 18, ……..
6 + x = 3k where k is any integer.
For k = 0,
6 + x = 3 × 0
⇒ 6 + x = 0
x = -6. Not possible
For k = 1,
6 + x = 3 × 1
⇒ 6 + x = 3
⇒ x = 3 – 6 = -3. Not possible
For k = 2,
6 + x = 3 × 2
⇒ 6 + x = 6
⇒ x = 6 – 6 = 0
2 + 4 + 0 = 6 multiple of 3
For k = 3,
6 + x = 3 × 3
⇒ x = 9 – 6 = 3
2 + 4 + 3 = 9 multiple of 3
For k = 4,
6 + x = 3 × 4
⇒ 6 + x = 12
⇒ x = 12 – 6 = 6
2 + 4 + 6 = 12 which is multiple of 3
For k = 5,
6 + x = 3 × 5
⇒ x = 15 – 6 = 9
2 + 4 + 9 = 15 which is multiple of 3
For k = 6,
6 + x = 3 × 6
⇒ x = 18 – 6 = 12 not possible as x is digit
Hence the required values of x are 0, 3, 6 or 9.

Ex 16.2 Class 8 Maths Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the value of z?
Solution:
A number is a multiple of 3 if the sum of its digits is divisible by 3.
3 + 1 + z + 5 = 3k where k is an integer
⇒ 9 + z = 3k
⇒ z = 3k – 9
Here, k = 0, 1, 2 is not possible as z is a digit of the number.
For k = 3,
z = 3 × 3 – 9 = 9 – 9 = 0
9 + 0 = 9 multiple of 3
For k = 4,
z = 3 × 4 – 9 = 12 – 9 = 3
9 + 3 = 12 multiple of 3
For k = 5,
z = 3 × 5 – 9 = 15 – 9 = 6
9 + 6 = 15 multiple of 3
For k = 6,
z = 3 × 6 – 9 = 18 – 9 = 9
9 + 9 = 18 multiple of 3
For k = 7,
z = 3 × 7 – 9 = 21 – 9 = 12 not possible as z is a digit
Hence, the required values of 2 are 0, 3, 6 and 9.

Playing with Numbers Class 8 Extra Questions Maths Chapter 16

Extra Questions for Class 8 Maths Chapter 16 Playing with Numbers

Playing with Numbers Class 8 Extra Questions Very Short Answer Type

Question 1.
Write the following numbers in generalised form.
(a) ab
(b) 85
(c) 132
(d) 1000
Solution:
(a) ab = 10 × a + 1 × b = 10a + b
(b) 85 = 10 × 8 + 1 × 5 = 10 × 8 + 5
(c) 132 = 100 × 1 + 10 × 3 + 1 × 2 = 100 × 1 + 10 × 3 + 2
(d) 1000 = 1000 × 1

Question 2.
Write the following in usual form.
(a) 3 × 100 + 0 × 10 + 6
(b) 5 × 1000 + 3 × 100 + 2 × 10 + 1
Solution:
(a) 3 × 100 + 0 × 10 + 6 = 300 + 0 + 6 = 306
(b) 5 × 1000 + 3 × 100 + 2 × 10 + 1 = 5000 + 300 + 20 + 1 = 5321

Question 3.
Which of the following numbers are divisible by 3?
(i) 106
(ii) 726
(iii) 915
(iv) 1008
Solution:
(i) Sum of the digits of 106 = 1 + 0 + 6 = 7 which is not divisible by 3.
Hence 106 is not divisible by 3.
(ii) Sum of the digits of 726 = 7 + 2 + 6 = 15 which is divisible by 3.
Hence 726 is divisible by 3.
(iii) Sum of the digits of 915 = 9 + 1 + 5 = 15 which is divisible by 3.
Hence 915 is divisible by 3.
(iv) Sum of the digits of 1008 = 1 + 0 + 0 + 8 = 9 which is divisible by 3.
Hence 1008 is divisible by 3.

Question 4.
Prove that the sum of the given numbers and the numbers obtained by reversing their digits is divisible by 11.
(a) 89
(b) ab
(c) 69
(d) 54
Solution:
(a) Given number = 89
Number obtained by reversing the order of digits = 98
Sum = 89 + 98 = 187 ÷ 11 = 17
Hence, the required number is 11.

(b) Given number = ab = 10a + b
Number obtained by reversing the digits = 10b + a
Sum = (10a + b) + (10b + a)
= 10a + b + 10b + a
= 11a + 11b
= 11(a + b) ÷ 11
= a + b

(c) Given number = 69
Number obtained by reversing the digits = 96
Sum = 69 + 96 = 165 ÷ 11 = 15
Hence, the required number is 11.

(d) Given number = 54
Number obtained by reversing the digits = 45
Sum = 54 + 45 = 99 ÷ 11 = 9
Hence, the required number is 11.

Question 5.
Prove that the difference of the given numbers and the numbers obtained by reversing their digits is divisible by 9.
(i) 59
(ii) xy
(iii) xyz
(iv) 203
Solution:
(i) Given number = 59
Number obtained by reversing the digits = 95
Difference = 95 – 59 = 36 ÷ 9 = 4
Hence, the required number is 9.

(ii) Given number = xy = 10x + y
Number obtained by reversing the digits = 10y + x
Difference = (10x + y) – (10y + x)
= 10x + y – 10y – x
= 9x – 9y
= 9(x – y) ÷ 9
= x – y
Hence, the required number is 9.

(iii) Given number = xyz = 100x + 10y + z
Number obtained by reversing the digits = 100z + 10y + x
Difference = (100x + 10y + z) – (100z + 10y + x)
= 100x + 10y + z – 100z – 10y – x
= 99x – 99z
= 99(x – z)
= 99(x – 2) ÷ 9
= 11 (x – z)
Hence, the required number is 9.

(iv) Given number = 203
Number obtained by reversing the digits = 302
Difference = 302 – 203 = 99 ÷ 9 = 11
Hence, the required number is 9.

Question 6.
If a, b, c are three digits of a three-digit number, prove that abc + cab + bca is a multiple of 37.
Solution:
We have abc + cab + bca
abc = 100a + 10b + c
cab = 100c + 10a + b
bca = 100b + 10c + a
Adding abc + cab + bca = 111a +111b + 111c
= 111 (a + b+ c)
= 37 × 3 (a + b + c) which is a multiple of 37.
Hence proved.

Playing with Numbers Class 8 Extra Questions Short Answer Type

Question 7.
Complete the magic square given below so that the sum of the numbers in each row or in each column or along each diagonal is 15.

Solution:
(i) A = 15 – (8 + 1) = 15 – 9 = 6
(ii) F = 15 – (8 + 5) = 15 – 13 = 2
(iii) C = 15 – (A + F) = 15 – (6 + 2) = 15 – 8 = 7
(iv) E = 15 – (1 + 5) = 15 – 6 = 9
(v) D = 15 – (E + F) = 15 – (9 + 2) = 15 – 11 = 4
(vi) B = 15 – (8 + 4) = 15 – 12 = 3
Hence the required square is

Question 8.
Find the values of P and Q from the given addition problem

Solution:
Here, 3 + Q = 7
⇒ Q = 7 – 3 = 4
Now taking second column, we get
4 + 7 = 11 i.e. 1 is carried over to third column
⇒ 1 + P + 2 = 9
⇒ 3 + P = 9
P = 9 – 3 = 6
Hence the value of P = 6 and Q = 4

Question 9.
Find the values of p, q and r in the following multiplication problem.

Solution:
6 × 4 = 24, Here 2 is carried over second column
⇒ 6 × p + 2 – 3 × 10 = 2 [∵ 21 – 3 × 6 = 3]
⇒ 6p – 30 = 0
⇒ p = 5
Now the multiplication problem becomes,

Here 2 + r = 4
⇒ r = 2
q × 354 = 1062
⇒ q = 3
Hence, p = 5, q = 3, r = 2

Question 10.
Observe the following patterns:
1 × 9 – 1 = 8
21 × 9 – 1 = 188
321 × 9 – 1 = 2888
4321 × 9 – 1 = 38888
Find the value of 87654321 × 9 – 1
Solution:
From the pattern, we observe that there are as many eights in the result as the first digit from the right which is to be multiplied by 9 and reduced by 1.
87654321 × 9 – 1 = 788888888

Playing with Numbers Class 8 Extra Questions High Order Thinking Skills (HOTS) Type

Question 11.
Complete the cross number puzzle with the given column.


Solution:

Hence the complete square is

Question 12.
The product of two 2-digit numbers is 1431. The product of their tens digits is 10 and the product of their units digits is 21. Find the numbers. Solution:
Let the required two 2-digit numbers be 10a + b and 10p + q as per the condition, we have
a × p = 10 and b × q = 21
a = 2 and p = 5 or a = 5 and p = 2
Similarly b × q = 21
b = 3 and q = 7 or b = 7 and q = 3
10p + q = 57 or 10p + q = 53
and 10a + b = 23 or 10a + b = 27
Since the units digit of product 1431 is 1.
Numbers are 57 and 23 or 53 and 27.
Now 57 × 23 = 1311 and 53 × 27 = 1431 which is given.
Hence, the required numbers are 53 and 27.