Extra Questions for Class 10 Maths Chapter 4 Quadratic Equations. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

You can also download Class 10 Maths to help you to revise complete syllabus and score more marks in your examinations.

Quadratic Equations Class 10 Extra Questions Very Short Answer Type

Question 1.
For what value of V the quadratic equation 9x² – 3ax + 1 = 0 has equal roots?
Or
If one root of the quadratic equation 2x² + 2x + k = 0 is – 13\frac{1}{3}, then find the value of k. [CBSE 2019]
Answer:
For equal roots D = 0
where D = b² – 4ac
Here a = 9, b = – 3a, c = 1
∴ (- 3a)² – 4(9) (1) = 0
⇒ 9a² – 36 = 0
⇒ 9(a² – 4) = 0
⇒ a² = 4
⇒ a = ± 2
Or
Let, p(x) = 2x² + 2x + k

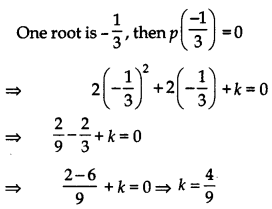
Question 2.
For what values of k, the roots of the equation x² + 4x + k = 0 are real?
Or
Find the value of k for which the roots of the equation 3x² – 10x + k = k = 0 are reciprocal of each other. [CBSE 2019]
Answer:
For real roots D ≥ 0 i.e., b² – 4ac ≥ 0
Here, a = 1, b = 4, c = k
∴ (4)² – 4(1)k ≥ 0
⇒ 16 – 4k ≥ 0 ⇒ k ≤ A
Or
Roots of the equation 3x² – 10x + k = 0 are reciprocal of each other
⇒ Product of roots = 1
⇒ ca=k3 = 1 ⇒ k = 3

Question 3.
If the roots of quadratic equation px² + 6x + 1 = 0 are real, then find p.
Answer:
Roots are real, D ≥ 0
b² – 4ac ≥ 0
(6²) – 4 × p × 1 ≥ o
9 ≥ p

Question 4.
If 7x² – (2p² – 8)x + 16 = 0 has two roots which are equal in magnitude but opposite in sign then find p.
Answer:
Let the roots be α and – α.

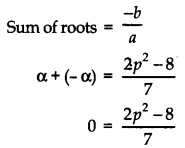
0 = 2p² – 8
p² = 4
p = ±2

Quadratic Equations Class 10 Extra Questions Short Answer Type-1

Question 1.
Find the roots of the quadratic equation
√2x² + 7x + 5√2 = 0 [CBSE Delhi 2017]
Answer:
√2x² + 7x + 5√2 = 0
√2x² + 2x + 5x + 5√2 = 0
⇒ (√2x + 5) (x + √2) = 0
⇒ x = −52√, – √2
or −52√2, – √2

Question 2.
Find the value of k for which the equation x² + k(2x + k – 1) + 2 = 0 has real and equal roots.
Answer:
Rewriting given equation as
x² + 2kx + (k² – k + 2) = 0
Here a = 1, b = 2k, c = k² – k + 2
For equal roots, b² – 4ac = 0
⇒ (2k)² – 4(1) (k² – k + 2) = 0

⇒ k = 2

Question 3.
If – 5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, find the value of k. [CBSE Outside Delhi 2016]
Answer:
– 5 is root of the equation 2x² + px – 15 = 0, then
2(-5)² + p(-5) – 15 = 0
⇒ 50 + (- 5)p – 15 = 0
⇒ p = −35−5 = 7 ……….. (1)
p(x² + x) + k = 0 has equal root
⇒ b² – 4ac = 0
Here b = p, a = p, c = k
⇒ p² = 4 pk ………….. (2)
(7)² – 4 × 7k = 0
(1) and (2) gives,
∴ k = 74

Question 4.
For what value of k, x² + 4x + k is a perfect square?
Answer:
A quadratic expression is a perfect square, if and only if corresponding equation has equal roots.
i.e., D = 0
⇒ 16 – 4k = 0
⇒ k = 4

Question 5.
Solve: 1a+b+x=1a+1b+1x,
[x ≠ 0, x ≠ – (a + b)].
Answer:

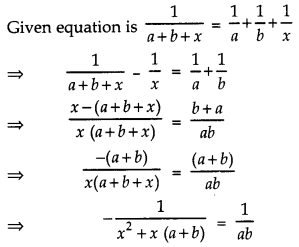
⇒ – ab = x² + x (a + b)
⇒ x² + x (a + b) + ab = 0
⇒ x² + ax + bx + ab = 0
⇒ x (x + a) + b (x + a) = 0
⇒ (x + a) (x + b) = 0
∴ x = – a or x = – b
Hence, – a and – b are roots of given equation.

Question 6.
The product of two consecutive positive integers is 306. Find the integers.
Answer:
Let the consecutive positive integers be x and x + 1.
Then, x (x + 1) = 306
or, x² + x – 306 = 0
or, x² + 18x – 17x – 306 = 0
or, x(x + 18) – 17(x + 18) = 0
or, (x + 18) (x – 17) = 0
x = – 18, 17
Neglecting x = – 18
∴ x = 17 and x + 1 = 17 + 1 = 18
Hence, two consecutive positive integers are 17 and 18.

Quadratic Equations Class 10 Extra Questions Short Answer Type-2

Question 1.
If the equation (1 + m²)x² + 2 mcx + c² – a² = 0 has equal roots then show than c² = a² (1 + m²). [CBSE 2017]
Answer:
(1 + m²) x² + 2mcx + c² – a² = 0
Here A = (1 + m²), B = 2mc, C = c² – a²
For equal roots; B² – 4AC = 0
⇒ (2mc)² – 4(1 + m²) (c² – a²) = 0

⇒ c² – a²(1 + m²) = 0
⇒ c² = a²(1 + m²)

Question 2.
Solve for x:
2xx−3+12x+3+3x+9(x−3)(2x+3) = 0, x ≠ 3, – 32. [CBSE Delhi 2016]
Answer:
Given:

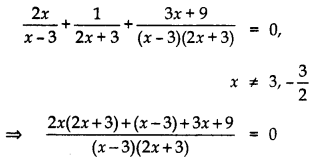
⇒ 4×2 + 6x + x- 3 + 3x + 9 = 0
⇒ 4×2 + lOx + 6 = 0
⇒ 4×2 + 4x+ 6x + 6 = 0
⇒ 4x(x + 1) + 6(x + 1) = 0
⇒ (x +1) (4x + 6) = 0
⇒ x + 1 = 0
or 4x + 6 = 0
⇒ x = – 1, – 32
But
x ≠ – 32

Question 3.
A plane left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.
Answer:
Let the usual speed of plane be x km/hr
∴ [Time taken to travel 1500 km with speed × km/hr] – [Time taken to travel 1500 km with speed (x + 100) km/hr] = half an hour

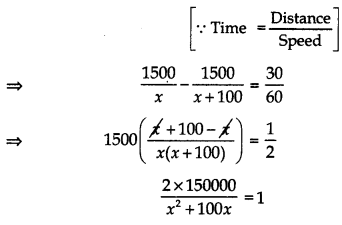
⇒ x² + 100x – 300000 = 0
x² + 600x – 500x – 300000 = 0
(x + 600) (x – 500) = 0
x = 500 as x can’t be negative so – 600 is rejected.
∴ usual speed of the plane is 500 km/hr.

Question 4.
Find the value of p for which the quadratic equation (2p + 1)x² – (7p + 2)x + (7p – 3) = 0 has equal roots. Also find these roots. [S.A-II, 2014]
Answer:
(2p + 1)x² – (7p + 2)x + (7p – 3) = 0 …(1)
For equal roots D = 0
b² – 4ac = 0
⇒ [- (7p + 2)]² – 4(2p + 1) (7p – 3) = 0
⇒ 49p² + 4 + 28p – 4 (14p² – 6p + 7p – 3) = 0
⇒ 49p² + 28p + 4 – 56p2 + 24p – 28p + 12 = 0
⇒ – 7p² + 24p + 16 = 0
⇒ 7p² – 24p – 16 = 0
⇒ 7p² – 28p + 4p – 16 = 0
⇒ 7p (p – 4) + 4 (p – 4) = 0
⇒ (p – 4) (7p + 4) = 0
∴ p = 4, −47
If p = 4, then (1)
⇒ 9x² – 30x + 25 = 0
⇒ 9x² – 15x – 15x + 25 = 0
⇒ 3x(3x – 5) – 5(3x – 5) = 0
⇒ (3x – 5) (3x – 5) = 0
⇒ (3x – 5)² = 0
⇒ 3x – 5 = 0
∴ x = 53
∴ Roots are 53 and 53.
If P = – 47, then (1)
⇒ −x27 + 2x – 7 = 0
– x² + 14x – 49 = 0
x² – 14x + 49 = 0
(x – 7)² = 0
∴ x = 7, 7

Question 5.
A journey of 192 km from a town A to town B takes 2 hours more by a ordinary passenger train than a super fast train. If the speed of the faster train is 16 km/h more, find the speeds of the faster and the passenger train.
Answer:
Let the speed of passenger train be x km/h.
Then, speed of faster train = (x + 16) km/h
According to question:
Time taken to complete the journey by faster train (t₁) = 192x+16 hours and time taken by passenger train (t₂) = 192x
According to question,

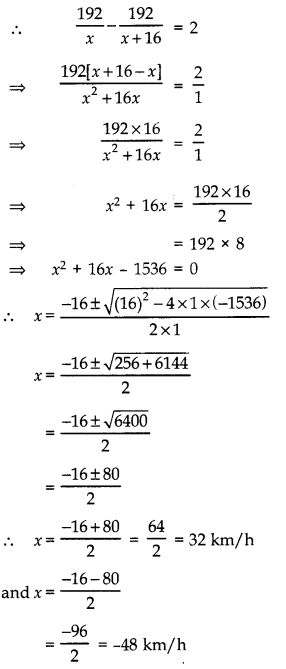
∵ Speed cannot be negative.
∴ Speed of the passenger train = 32 km/h
and speed of faster train = 32 + 16 = 48 km/h

Quadratic Equations Class 10 Extra Questions Long Answer Type 1

Question 1.
Speed of a boat in still water is 15 kn\h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream. [CBSE Delhi 2017]
Answer:
Let speed of boat be xkm/hr
∴ Speed of boat upstream = (15 – x) km/hr.

200 = 225 – x²
⇒ x² = 25
x = 5 (Rejecting – 5)
∴ Speed of stream = 5 km/hr

Question 2.
Find x in terms of a, b and c:
ax−a+bx−b=2cx−c, x ≠ a, b, c [CBSE Delhi 2016]
Answer:
Consider the given equation:

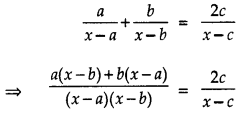
⇒ (x – c)[a(x – b) + b(x – a)] = 2c(x – a)(x – b)
⇒ (x – c)[ax – ab + bx – ab] = 2c(x² – bx – ax + ab)
⇒ ax² – 2abx + bx² – acx + 2abc – bcx = 2cx² – 2bcx – 2acx + 2abc
⇒ ax² + bx² – 2cx² = 2abx – acx – bcx
⇒ (a + b – 2c)x² = x(2ab – ac – bc)
⇒ (a + b – 2c)x² – x(2ab – ac – bc) = 0
⇒ x[(a + b – 2c)x – (2 ab – ac – bc) = 0
⇒ either x = 0
or (a + b – 2c)x – (2ab – ac – bc) = 0
or (a + b – 2c)x = (2ab – ac – bc)
or x = (2ab−ac−bc)(a+b−2c)
Thus, the two roots of the given equation are x = 0 and 

Question 3.
A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed. If it takes 3 hours to complete total journey, what is the original average speed ? [CBSE 2018]
Answer:
Let original speed of train be x km/ hr
Distance = 63 km; time (t₁) = 63/x hrs
∴ Faster speed = (x + 6) km/hr
[∵ Time =  Distance  Speed ]
Distance = 72 km; time (t₂) = 72/ (x + 6) hrs.
(t₁) + (t₂) = 3 hrs
63x+72(x+6) = 3
⇒ 63(x + 6) + 72x = 3x (x + 6)
⇒ 63x + 378 + 72x = 3x² + 18x
⇒ 3x² – 117x – 378 = 0
⇒ x² – 39x – 126 = 0
⇒ 7x² – 42x + 3x + 126 = 0
⇒ (x – 42) (x + 3) = 0
⇒ x = -3
[Rejected as speed can’t be negative]
∴ x = 42
∴ Original speed of train is 42 km/hr.

Question 4.
A motor boat whose speed is 18 km/hr in still water takes 1 hr more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. [CBSE 2018]
Answer:
Let the speed of stream be x km/ hr
∴ The speed of the boat upstream = (18 – x) km/hr
and speed of the boat downstream = (18 + x) km/hr
According to the question:

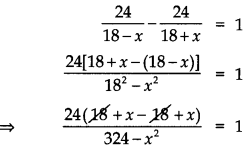
⇒ 48x = 324 – x²
⇒ x² + 48x – 324 = 0
⇒ x² + 54x – 6x – 324 = 0
⇒ x(x + 54) – 6(x + 54) = 0
⇒ (x + 54) (x – 6) = 0
⇒ x + 54 = 0
x = – 54
[Rejecting – 54, as speed can’t be negative]
and x – 6 = 0
∴ x = 6 km/h
∴ Speed of the stream = 6 km/hr.

Question 5.
A thief runs with a uniform speed of 100 m/ minute. After one minute, a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief? [CBSE 2016]
Answer:
Suppose the policeman catches the thief after t minutes.
Uniform speed of the thief = 100 metres/minute
∴ Distance covered by thief in (t + 1) = 100 (t + 1) metres [∵ Distance = Speed × Time]
Distance covered by policeman in t minutes = Sum of t terms of an AP with first term 100 and common difference 10.
t2 [2 × 100 + (t -1) × 10] m
= t[100 + 5(t – 1)]
= t(5t + 95) = 5t² + 95t
When the policeman catches the thief.
5t² + 95t = 100 (t + 1)
⇒ 5t² + 95t = 100t + 100
⇒ 5t² – 5t – 100 = 0
⇒ t² – t – 20 = 0
⇒ t = – 4 and t = 5
Neglecting -ve time. We get t = 5
Thus, the policeman catches the thief after 5 minutes.

Question 6.
The difference of two natural numbers is 5. If the difference of their reciprocals is 110, find the two numbers.
Answer:
Let the number be x and y (x > y).
According to question; x – y = 5 …………… (i)

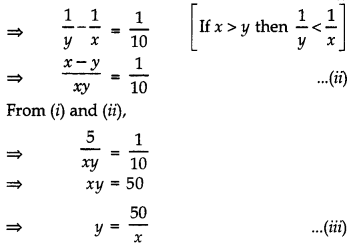
Putting the value of y in (z)
x – 50x =5
⇒ x² – 50 = 5x
⇒ x² – 5x – 50 = 0
⇒ x2² – 10x + 5x – 50 = 0
⇒ x (x – 10) + 5 (x – 10) = 0
⇒ (x – 10) (x + 5) = 0
⇒ x = – 5, 10
When x = – 5, y = 50−5 = – 10
When x = 10, y = 5010 = 5
∴ Two natural numbers as 5,10.

Quadratic Equations Class 10 Extra Questions HOTS

Question 1.
Solve 5+5+5+…−−−−−−√−−−−−−−−−−√−−−−−−−−−−−−−−−√
Answer:
Let x = 5+5+5+…−−−−−−√−−−−−−−−−−√−−−−−−−−−−−−−−−√
⇒ x = 5+x−−−−√
Squaring both sides, we get
x² = 5 + x
⇒ x² – x – 5 = 0

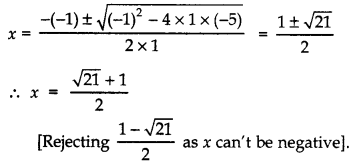
Question 2.
Solve by factorisation: (x – 3) (x – 4) = 34332
Answer:

Question 3.
If the equation (1 + m²) x² + 2mcx + c² – a² = 0 has equal roots, show that c² = a² (1 + m²).
Answer:
Given equation is,
(1 + m²) x² + 2mcx + c² – a² = 0
∵ Roots are equal.
∴ D = 0
B² – 4AC = 0
(2mc)² – 4 (1 + m²) (c² – a²) = 0
or 4m²c² – 4 [c² – a² + m²c² – m²a²] = 0
or 4[m²c² – c² + a² – m²c² + m²a²] = 0
or – c² + a² (1 + m²) = 0
or c² = a² (1 + m²).

Question 4.
A person on tour has ₹ 360 for his expenses. If he extends his tour for 4 days, he has to cut down his daily expenses by ₹ 3. Find the original duration of the tour.
Answer:
Let, original duration of tour = x days
Expenditure on tour = ₹ 360
So, expenditure per day = ₹ 360x
According to 1st condition,
Duration of extended tour = (x + 4) days
Expenditure per day = ₹ 360x+4
According to 2nd condition,
360x−360x+4 = 3
360 (x + 4) – 360x = 3x (x + 4)
360x + 1440 – 360x = 3 (x² + 4x)
x² + 4x – 480 = 0, S = 4
x² + 24x – 20x – 480 = 0, P = – 480
x(x + 24) – 20 (x + 24) = 0
(x + 24) (x – 20) = 0
Either x + 24 = 0 or x – 20 = 0
x = – 24 or x = 20
∵ x cannot be negative so, x = 20
Hence, original duration of tour has 20 days.

Question 5.
The hypotenuse of a right triangle is 1 m less than twice the shortest side. If the third side is 1 m more than the shortest side, find the sides of the triangle.
Answer:
Let, shortest side of triangle = x m
Hypotenuse of triangle = (2x – 1) m
Third side of triangle = (x + 1) m By
Pythagoras theorem,
(Hyp.)² = (Base)² + (Alt.)²
(2x – 1)² = (x + 1)² + (x)²
4x² + 1 – 4x = x² + 1 + 2x + x²
2x² – 6x = 0
2x (x – 3) = 0
Either 2x = 0 or x – 3 = 0
x = 0 or x = 3
But side cannot be zero, so . x = 3
∴ Shortest side = x = 3 m
Hypotenuse = (2x – 1) = [2 (3) – 1] = 5 m
Third side = x + 1 = (3 + 1) = 4 m.

Multiple Choice Questions

Choose the correct option for each of the following:

Question 1.
The condition on ‘a’ for ax² + bx + c = 0 to represent a quadratic equation is:
(a) a = 0
(b) a > 0
(c) a < 0
(d) a ≠ 0
Answer:
(d) a ≠ 0

Question 2.
The value of k for which the expression x² + 4x + k is a perfect square is :
(a) 4
(b) – 4
(c) 16
(d) 3
Answer:
(a) 4

Question 3.
Which of the following equation has 3 as a root?
(a) x² – 4x + 2 = 0
(b) x² + x – 3 = 0
(c) 2x² – 8x + 6 = 0
(d) 3x² – 6x – 2 = 0
Answer:
(c) 2x² – 8x + 6 = 0

Question 4.
If 13 is a root of x² + kx – 1 = 0, then value of k is:
(a) 43
(b) 83
(c) 13
(d) – 3
Answer:
(b) 83

Question 5.
Which of the following is true about the equation 1x2−3x+5 = 1
(a) Its discriminant is not defined
(b) Its discriminant is – 7
(c) Its discriminant is -11
(d) Its discriminant is same as coefficient of x
Answer:
(b) Its discriminant is – 7

Question 6.
Which of the following is not a quadratic equation?
(a) 12x2−x+1 = – 2
(b) (x² – 1)² = x^4& + 31 + 4x²
(c) 2(x – 1)² = 4x² – 3x + 1
(d) (√3x + √5)² + x² = 4x² – 5x
Answer:
(d) (√3x + √5)² + x² = 4x² – 5x

Question 7.
The roots of the equation ax² + bx + c = 0 are non- real, if
(a) b² – 4ac = 0
(b) b² – 4ac < 0
(c) b² – 4ac > 0
(d) coefficient of x is zero
Answer:
(b) b² – 4ac < 0

Question 8.
The roots of equation ax² + bx + c = 0, a ≠ 0 are real, if b² – 4ac is
(a) = 0
(b) ≥ 0
(c) ≤ 0
(d) none of these
Answer:
(b) ≥ 0

Question 9.
If n denotes the number of roots of a quadratic equation, then
(a) n is always equal to 2
(b) n < 2 (c) n ≤ 2 (d) n > 2
Answer:
(c) n ≤ 2

Question 10.
The positive value of /c for which the equation x² + kx + 9 = 0 and x² – 12x + k = 0 will both have real roots
(a) 36
(b) 6
(c) 16
(d) 12
Answer:
(b) 6

Question 11.
The equation (a² + b²)x² – 2 (ac + bd) x + c² + d² = 0 has equal roots, then
(a) ab = cd
(b) ad = bc
(c) ad = √bc
(d) ad = √cd
Answer:
(d) ad = √cd

Question 12.
The sum of a number and its reciprocal is 10/3, then the number is:
(a) 1
(b) 2
(c) 3
(d) 5
Answer:
(c) 3

Question 13.
The value of k for which – 5 is a root of 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots is
(a) 32
(b) 37
(c) 74
(d) 14
Answer:
(c) 74

Question 14.
What constant should be added or subtracted to solve the quadratic equation x² – 5√2x – 4 = 0 by the method of completing the square?
(a) 54
(b) 516
(c) 5√4
(d) 254
Answer:
(b) 516

Question 15.
The value of k for which roots of kx² – 3x + 1 = 0 are real is .
(a) k ≥ 94
(b) k ≤ −94
(c) k ≤ 94
(d) k ≤ 32
Answer:
(c) k ≤ 94

Fill in the blanks:

Question 1.
Quadratic equation ax² + bx + c = 0 has two _____________ and _____________ roots if b² – 4ac > 0.
Answer:
real, unequal

Question 2.
Quadratic equation ax² + bx + c = 0 has two real and _____________ roots if b² – 4ac = 0.
Answer:
equal

Question 3.
For a quadratic equation ax² + bx + c = 0, the quantity b² – 4ac is called _____________ .
Answer:
discriminant

Question 4.
Quadratic equation ax² + bx + c = 0 has two _____________ roots if b² – 4ac < 0. Answer: imaginary Question 5. If D > 0 and is a perfect square then roots are _____________ (rational/irrational/imaginary).
Answer:
rational

Question 6.
If D > 0 and it is not a perfect square then roots are _____________ (rational/irrational/imaginary).
Answer:
irrational

Question 7.
If the value of mα² + nα + p is zero, then a is said to be the _____________ of equation mx² + nx + p = 0.
Answer:
root

Question 8.
The quadratic formula for finding roots of equation ax² + bx + c = 0 is given by _____________ .
Answer:
x = −b±b2−4ac√2a

Question 9.
A quadratic equation can have at most _____________ roots.
Answer:
two

Question 10.
The quadratic equation x² – 3x + 5 = 0 has _____________ roots.
Answer:
imaginary