Importance of Algebra

Algebra helps in the representation of problems as mathematical expressions.  All the branches of mathematics such as trigonometry, calculus, coordinate geometry, involve using algebra. One simple example of an expression of algebra is 3x + 5 = 12.

Algebra deals with symbols that are related to each other with the help of operators. It is not just a mathematical concept, but a skill that all of us use in our daily life without even realizing it. Understanding the concept of algebra is more important than solving equations and finding the right answer, as it is useful for all the topics of mathematics that you will learn in the future or you have already learned it in past.

What Is Algebra Actually?

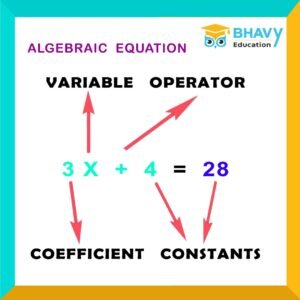
Algebra is a branch of math that deals with symbols and arithmetic operations. These symbols don’t have a fixed value and are called variables. In real-life problems, we often see certain values that keep changing. But there is a constant need to represent these changing values. In algebra, these values are often represented by symbols such as a, b, c, p, or q, and these symbols are called variables. Further, these symbols are manipulated using various arithmetic operations of addition, subtraction, multiplication, and division, with an objective to find the values.The algebraic expressions given below are made up of variables, operators, and constants. Here the numbers 3, 25 are constants, x is the variable, and the arithmetic operation of addition is performed.

Branches of Algebra 

The complexity of algebra is simplified by the use of numerous algebraic expressions. Based on the use and the complexity of the expressions, algebra is classified into various branches that are listed below:                     

 

 

• Pre-algebra
• Elementary Algebra
• Abstract Algebra
• Universal Algebra
• Pre-algebra

The basic way of presenting the unknown values as variables helps to create mathematical expressions. It helps in transforming real-life problems into an algebraic expression in mathematics. Forming a mathematical expression of the given problem statement is a part of pre-algebra.

Elementary Algebra

Elementary algebra deals with the solving of the algebraic expressions for a variable answer. In elementary algebra, simple variables like x, y, z are represented in the form of equations. Based on the degree of the variable, equations are called linear equations, quadratic equations, polynomial. Linear equation is of the form of ax + b = c, ax + by + c = 0, ax + by + cz + d = 0. Elementary algebra is based on the degree of the variables, branches out into quadratic equations and polynomials. A general form of representing a quadratic equation is ax² + bx + c = 0, and for a polynomial equation, it is axⁿ + bx^n-1+ cx^n-2+ …..k = 0.

Abstract Algebra

Abstract algebra deals with the use of abstract concepts like rings, groups, vectors rather than simple mathematical numbers. Rings are a simple level of abstraction found by writing addition and multiplication properties together. Group theory and ring theory are the two important concepts of abstract algebra. Abstract algebra finds numerous applications of computer sciences, physics, astronomy, and uses vector spaces to represent quantities.

Universal Algebra

All other mathematical forms involving calculus, trigonometry, coordinate geometry involving algebraic expressions can be accounted as universal algebra. Across these topics, universal algebra studies mathematical expression and doesn’t involve the study of models of algebra. All the other branches of algebra can be considered a subsets of universal algebra. Any real-life problem can be classified into one of the branches of mathematics and can be solved using abstract algebra.

Algebra Topics       

Algebra is divided into numerous topics to help for a detailed study. Here we have listed below some of the important topics of algebra such as sequence and series, algebraic expressions and equations, logarithm, exponents, and sets

Algebraic Expressions

An algebraic expression is formed using integer constants, variables, and basic arithmetic operations. An example of an algebraic expression is 4x + 6. Here 4 and 6 are fixed numbers and x is a variable. Further, the variables can be simple variables using alphabets like x, y, z or can have complex variables like x², x³, xⁿ, xy, x²y, etc. Algebraic expressions are also known as polynomials. A polynomial is an expression consisting of variables, coefficients, and non-negative integer exponents of variables. Example: 2x³ + 3x² + 8x + 7 = 0.

(image)

An equation is a mathematical statement that has an ‘equal to’ symbol between two algebraic expressions that have equal values. Given below are the different equations, based on the degree of the variable, where we apply the concept of algebra:

• Linear Equations: Linear equations help in representing the relationship between variables such as x, y, z, and are expressed in exponents of degree one. In linear equations, we use algebra, starting from the basics such as the addition and subtraction of algebraic expressions.
• Quadratic Equations: The standard form of quadratic is ax² + bx + c = 0, where a, b, c are constants and x is the variable. The values of x that satisfy the equation are called solutions of the equation, and a quadratic equation has a maximum of two solutions.
• Cubic Equations: The algebraic equations having variables with power 3 are referred to as cubic equations. A general form of a cubic equation is ax³ + bx² + cx + d = 0. The cubic equation has numerous applications in three-dimensional geometry and calculus.

Algebraic Formulas

Algebraic identities are equations that are always true regardless of the values assigned to the variables. Identity means that the left-hand side of the equation is identical to the right-hand side, for all values of the variables. These formulae involve squares and cubes of algebraic expressions and help in solving the algebraic expressions in a few quick steps. The frequently used algebraic formulas are listed below.

• (a + b)²= a² + 2ab + b²
• (a – b)²= a²  – 2ab + b²
• (a + b)(a – b) = a²– b²
• (x + a)(x + b) = x + (a + b)x + ab
• (a + b + c)²= a² + b²+ c2 + 2ab + 2bc + 2ca
• (a + b)³= a³ + 3a²b + 3ab² + b³
• (a – b)³= a³ – 3a²b + 3ab² – b³

Let us see the application of these formulas in algebra using the following example,

Example: Using the (a + b)² formula in algebra, find the value of (101)².

Solution:

Given: (102)² = (100 + 2)²          
Using algebra formula (a + b)² = a² + 2ab + b², we have,
(100 + 2)² = (100)² + 2(2)(100) + (2)²
(102)² = 10404

Algebraic Operations

The basic operations covered in algebra are addition, subtraction, multiplication, and division.

• Addition: For the addition in algebra, two or more expressions are separated by a plus(+) sign between them.
• Subtraction: For the subtraction in algebra, two or more expressions are separated by a minus(-) sign between them.
• Multiplication: For the multiplication in algebra, two or more expressions are separated by a multiply(×) sign between them.
• Division: For the division in algebra, two or more expressions are separated by a “/” sign between them.

Basic Properties of Algebra

The basic properties of algebra for variables, algebraic expressions, or real numbers a, b and c are as given below,

• Commutative Property of Addition:- a + b = b + a
• Commutative Property of Multiplication:- a × b = b × a
• Associative Property of Addition:- a + (b + c) = (a + b) + c
• Associative Property of Multiplication:- a × (b × c) = (a × b) × c
• Distributive Property:- a × (b + c) = a × b + b × c or a × (b – c) = a × b – a × c
• Reciprocal:- Reciprocal of a = 1/a
• Additive Identity:- a + 0 = 0 + a = a
• Multiplicative Identity:- a × 1 = 1 × a = a
• Additive Inverse:- a + (-a) = 0